题目内容
9.已知点A(0,-4),B(8,0)和C(a,a),以线段AB的中点为圆心的圆过点C,则这个圆的半径的最小值等于3$\sqrt{2}$.分析 首先求得AB的中点D的坐标,然后求得经过点D且垂直于直线y=x的直线的解析式,然后求得与y=x的交点坐标,再求得交点与D之间的距离即可.
解答 解:理解过圆心C的直线与一次函数y=x垂直的交点即为这个圆的半径的最小值.
AB的中点D的坐标是:(4,-2).
∵C(a,a)在一次函数y=x上,
∴设过D且与直线y=x垂直的直线的解析式是y=-x+b,
把(4,-2)代入解析式得:-4+b=-2,
解得:b=2,
则函数解析式是y=-x+2.
根据题意得:$\left\{\begin{array}{l}{y=-x+2}\\{y=x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
则交点的坐标是(1,1).
则这个圆的半径的最小值是:$\sqrt{{(4-1)}^{2}{+(-2-1)}^{2}}$=3$\sqrt{2}$.
故答案是:3$\sqrt{2}$.
点评 此题考查一次函数的综合运用,两点之间的距离公式,以及两直线垂直的条件,正确理解C(a,a),一定在直线y=x上是解题的关键.

练习册系列答案
相关题目
19.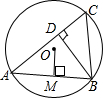 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC,垂足为D,OM⊥AB,垂足为M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC,垂足为D,OM⊥AB,垂足为M,则sin∠CBD的值等于( )
 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC,垂足为D,OM⊥AB,垂足为M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC,垂足为D,OM⊥AB,垂足为M,则sin∠CBD的值等于( )| A. | OM的长 | B. | OM的长的2倍 | C. | CD的长 | D. | CD的长的2倍 |
20.已知一元二次方程x2-6x-c=0有一个根为2,则另一个根为( )
| A. | 2 | B. | 3 | C. | 4 | D. | -8 |
14.计算4a6÷(-a2)的结果是( )
| A. | 4a4 | B. | -4a4 | C. | -4a3 | D. | 4a3 |
16. 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
(1)把上表中x,y的各组对应值作为点的坐标,在平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;.
(2)求销售价定为80元时,每日的销售利润.
 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:| x(元) | 60 | 65 | 70 | 75 | … |
| y (件) | 40 | 35 | 30 | 25 | … |
(2)求销售价定为80元时,每日的销售利润.
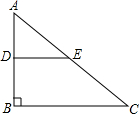 如图,在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,DE=4,则△ABC与△ADE的面积比为4:1.
如图,在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,DE=4,则△ABC与△ADE的面积比为4:1.