题目内容
11.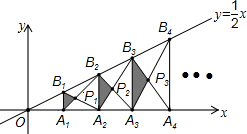 如图,已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn=$\frac{{n}^{2}}{8n+4}$(请用含n的代数式表示).
如图,已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn=$\frac{{n}^{2}}{8n+4}$(请用含n的代数式表示).
分析 根据图象上点的坐标性质得出点B1、B2、B3、…、Bn、Bn+1各点坐标,进而利用相似三角形的判定与性质得出S1、S2、S3、…、Sn,进而得出答案.
解答 解:∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,
∴依题意得:B1(1,$\frac{1}{2}$),B2(2,1),B3(3,$\frac{3}{2}$),…,Bn(n,$\frac{n}{2}$)
∵A1B1∥A2B2,
∴△A1B1P1∽△A2B2P1,
∴$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{\frac{1}{2}}{1}$=$\frac{1}{2}$,
∴△A1B1P1与△A2B2P1对应高的比为:1:2,
∵A1A2=1,
∴A1B1边上的高为:$\frac{1}{3}$,
∴SA1B1P1=$\frac{1}{2}$×$\frac{1}{3}$×$\frac{1}{2}$=$\frac{1}{12}$=$\frac{{1}^{2}}{8×1+4}$,
同理可得:SA2B2P2=$\frac{{2}^{2}}{8×2+4}$=$\frac{4}{20}$,
∴Sn=$\frac{{n}^{2}}{8n+4}$.
故答案为:$\frac{{n}^{2}}{8n+4}$.
点评 此题主要考查了一次函数函数图象上点的坐标性质得出B点坐标变化规律进而得出S的变化规律,得出图形面积变化规律是解题关键.

练习册系列答案
相关题目
19.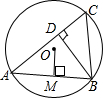 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC,垂足为D,OM⊥AB,垂足为M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC,垂足为D,OM⊥AB,垂足为M,则sin∠CBD的值等于( )
 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC,垂足为D,OM⊥AB,垂足为M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC,垂足为D,OM⊥AB,垂足为M,则sin∠CBD的值等于( )| A. | OM的长 | B. | OM的长的2倍 | C. | CD的长 | D. | CD的长的2倍 |
6.若分式$\frac{x-2}{x+1}$无意义,则x的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
20.已知一元二次方程x2-6x-c=0有一个根为2,则另一个根为( )
| A. | 2 | B. | 3 | C. | 4 | D. | -8 |
 如图所示,在Rt△ABC中,∠C=90°,AB=2AC,AD为∠BAC的平分线,求证:点D在线段AB的垂直平分线上.
如图所示,在Rt△ABC中,∠C=90°,AB=2AC,AD为∠BAC的平分线,求证:点D在线段AB的垂直平分线上.