题目内容
7.如图,所有小正方形的边长都为1,A、B、C都在格点上.(1)过点C画直线AB的平行线(仅利用所给方格纸和直尺作图,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段AG的长度是点A到直线BC的距离;线段AH的长度是点H到直线AB的距离.
(4)线段AG、AH的大小关系为:AG=$\frac{\sqrt{2}}{2}$AH.理由:△AGH是等腰直角三角形,.
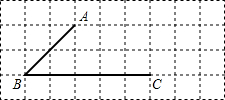
分析 (1)根据网格中AB所在位置过点C得出直线CQ∥AB即可;
(2)根据网格中点A所在的位置画出AG⊥BC,AH⊥AB即可;
(3)利用点到直线的距离定义得出答案;
(4)由等腰直角三角形的性质得到答案.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
(3)线段AG的长度是点A到直线BC的距离,线段AH的长度是点H到直线AB的距离;
故答案为:AG,AB;
(4)AG=$\frac{\sqrt{2}}{2}$AH,
理由:∵△AGH是等腰直角三角形,
∠AGH=90°AG=GH,
∵∠AHG=45°,
∴AG=$\frac{\sqrt{2}}{2}$AH.
故答案为:AG=$\frac{\sqrt{2}}{2}$AH,△AGH是等腰直角三角形.
点评 此题主要考查了基本作图以及点到直线的距离等知识,根据题意结合网格各点位置是解题关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
20.已知一元二次方程x2-6x-c=0有一个根为2,则另一个根为( )
| A. | 2 | B. | 3 | C. | 4 | D. | -8 |
2.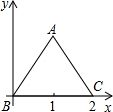 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )| A. | (1,$\sqrt{3}$) | B. | (1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
16.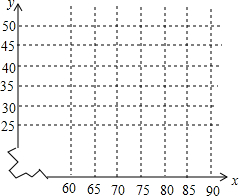 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
(1)把上表中x,y的各组对应值作为点的坐标,在平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;.
(2)求销售价定为80元时,每日的销售利润.
 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:| x(元) | 60 | 65 | 70 | 75 | … |
| y (件) | 40 | 35 | 30 | 25 | … |
(2)求销售价定为80元时,每日的销售利润.
17.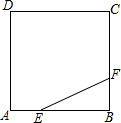 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )| A. | $6\sqrt{5}n+5\sqrt{5}$ | B. | $5\sqrt{5}n+\sqrt{5}$ | C. | $6\sqrt{5}n-5\sqrt{5}$ | D. | $5\sqrt{5}n-4\sqrt{5}$ |
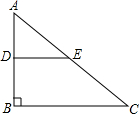 如图,在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,DE=4,则△ABC与△ADE的面积比为4:1.
如图,在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,DE=4,则△ABC与△ADE的面积比为4:1.