题目内容
19.若△ABC∽△A′B′C′,已知AB=6cm,A′B′=3cm,则△ABC与△A′B′C′的面积比为( )| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:1 |
分析 根据相似三角形的面积的比等于相似比的平方进行解答.
解答 解:∵△ABC∽△A′B′Cˊ,AB=6cm,A′B′=3cm,
∴其相似比=$\frac{AB}{A′B′}$=$\frac{6}{3}$=$\frac{2}{1}$,
∴△ABC与△A′B′C′的面积比=(AB:A′B′)2=4:1.
故选D.
点评 本题考查的是相似三角形的性质,熟知相似三角形面积的比等于相似比的平方是解答此题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
14.某市今年第一季度快递业务总量达到4210000件,4210000这个数字用科学记数法表示为( )
| A. | 0.421×107 | B. | 4.21×106 | C. | 4.21×107 | D. | 4.21×104 |
4. 如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
 如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )| A. | x>4或x<-2 | B. | -2<x<4 | C. | -2<x<3 | D. | 0<x<3 |
8. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )
 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①③④ |
9.设点A(x1,y1)和B(x2,y2)是反比例函数y=$\frac{k}{x}$图象上的两个点,当x1<x2<0时,y1<y2,则一次函数y=-2x+k的图象经过( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |
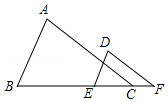 如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是∠B=∠DEC.(只需写一个条件,不添加辅助线和字母)
如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是∠B=∠DEC.(只需写一个条件,不添加辅助线和字母)