题目内容
11.先化简,再求值:($\frac{a+1}{{a}^{2}-1}$-$\frac{2}{{a}^{2}+a-2}$)÷$\frac{a}{a-1}$,其中a=$\sqrt{5}$.分析 先化简题目中的式子,然后将a的值代入化简后的式子即可解答本题.
解答 解:($\frac{a+1}{{a}^{2}-1}$-$\frac{2}{{a}^{2}+a-2}$)÷$\frac{a}{a-1}$
=$[\frac{a+1}{(a+1)(a-1)}-\frac{2}{(a+2)(a-1)}]×\frac{a-1}{a}$
=$[\frac{1}{a-1}-\frac{2}{(a+2)(a-1)}]×\frac{a-1}{a}$
=$\frac{1}{a}-\frac{2}{a(a+2)}$
=$\frac{a+2-2}{a(a+2)}$
=$\frac{a}{a(a+2)}$
=$\frac{1}{a+2}$,
当a=$\sqrt{5}$时,原式=$\frac{1}{\sqrt{5}+2}=\frac{\sqrt{5}-2}{(\sqrt{5}+2)(\sqrt{5}-2)}=\sqrt{5}-2$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
1.下列各式计算正确的是( )
| A. | (π-3.14)0=0 | B. | (-2x+y)(2x+y)=y2-4x2 | ||
| C. | (-2x2y)3=-6x6y3 | D. | 5a2-a2=4 |
2.截至“十二五末”,我国累计光伏装机量达到4318万千瓦,跃居世界第一.4318万用科学记数法表示为( )
| A. | 4.318×103 | B. | 4318×104 | C. | 4.318×107 | D. | 43.18×106 |
19.若△ABC∽△A′B′C′,已知AB=6cm,A′B′=3cm,则△ABC与△A′B′C′的面积比为( )
| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:1 |
6.小明同学在“百度”搜索引擎中输入“中国梦,我的梦”,搜索到与之相关的结果条数约为9900000,将9900000这个数用科学记数法表示为( )
| A. | 0.99×107 | B. | 9.9×105 | C. | 9.9×106 | D. | 99×105 |
1.若a<b,则下列各式中,错误的是( )
| A. | a-3<b-3 | B. | -a<-b | C. | -2a>-2b | D. | $\frac{1}{3}$a<$\frac{1}{3}$b |
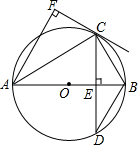 如图,AB为⊙O的直径,弦CD⊥AB,垂足为E,CF⊥AF,且CF=CE
如图,AB为⊙O的直径,弦CD⊥AB,垂足为E,CF⊥AF,且CF=CE