题目内容
8. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①△AED≌△GED;②四边形AEGF是菱形;③∠DFG=112.5°;④BC+FG=1.5,其中正确的结论是( )| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①③④ |
分析 首先证明△ADE≌△GDE,再求出∠AEF、∠AFE、∠GEF、∠GFE的度数,推出AE=EG=FG=AF,由此可以一一判断.
解答 证明:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DHG是由△DBC旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在RT△ADE和RT△GDE中,
$\left\{\begin{array}{l}{DE=DE}\\{DA=DG}\end{array}\right.$,
∴△AED≌△GED,故①正确,
∴∠ADE=∠EDG=22.5°,AE=EG,
∴∠AED=∠AFE=67.5°,
∴AE=AF,
在△AEF与△GEF中,$\left\{\begin{array}{l}{AE=GF}\\{∠AED=∠GED}\\{EF=EF}\end{array}\right.$,
∴△AEF≌△GEF,可得EG=GF,
∴AE=EG=GF=FA,
∴四边形AEGF是菱形,故②正确,
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°,故③正确.
∵AE=FG=EG=BG,BE=$\sqrt{2}$AE,
∴BE>AE,
∴AE<$\frac{1}{2}$,
∴CB+FG<1.5,故④错误.
故选B.
点评 本题考查正方形的性质、全等三角形的判定和性质、菱形的判定和性质、等腰直角三角形的性质等知识,解题的关键是通过计算发现角相等,学会这种证明角相等的方法,属于中考常考题型.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
18.若|x+y-5|与(x-y-1)2互为相反数,则x2-y2的值为( )
| A. | -5 | B. | 5 | C. | 13 | D. | 15 |
19.若△ABC∽△A′B′C′,已知AB=6cm,A′B′=3cm,则△ABC与△A′B′C′的面积比为( )
| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:1 |
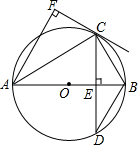 如图,AB为⊙O的直径,弦CD⊥AB,垂足为E,CF⊥AF,且CF=CE
如图,AB为⊙O的直径,弦CD⊥AB,垂足为E,CF⊥AF,且CF=CE