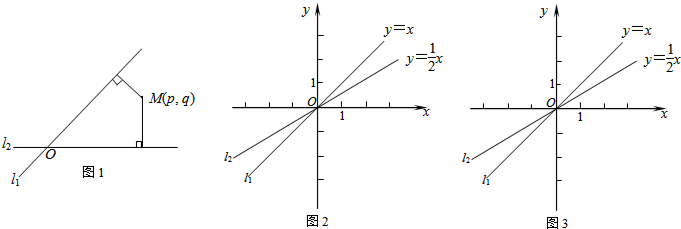
题目内容
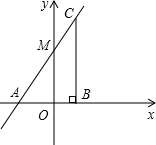 已知:如图,在直角坐标平面中,点A在x轴的负半轴上,直线y=kx+
已知:如图,在直角坐标平面中,点A在x轴的负半轴上,直线y=kx+| 3 |
| 3 |
(1)求这条直线的表达式;
(2)将△ABC绕点C旋转,使点A落到x轴上另一点D处,此时点B落在点E处.求点E的坐标.
考点:一次函数图象上点的坐标特征,坐标与图形变化-旋转
专题:
分析:(1)设A(-a,0),则B(a,0),直线BC的解析式为x=a,AB=2a,把点A代入可得出关于ka的表达式,由∠MAO=60°可表示出C点坐标,再根据点C在直线上可得出k、a的值,进而得出结论;
(2)根据题意画出图形,由k=
,a=1得出AB,AC,BC的长及C点坐标,过点E作EF⊥x轴于点F,根据△DEC由△ABC旋转而成得出CD=AC,DE=AB,根据相似三角形的判定定理得出△CBD∽△EFD,故
=
=
,由此可得出结论.
(2)根据题意画出图形,由k=
| 3 |
| DE |
| CD |
| EF |
| BC |
| DF |
| BD |
解答: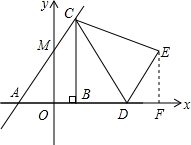 解:(1)设A(-a,0),则B(a,0),直线BC的解析式为x=a,AB=2a,
解:(1)设A(-a,0),则B(a,0),直线BC的解析式为x=a,AB=2a,
∵点A在直线y=kx+
上,
∴-ka+
=0①.
∵∠MAO=60°,
∴BC=ABtan60°=2a×
=2
a,
∴C(a,2
a),AC=4a,
∵点C在直线AC上,
∴ka+
=2
a②,
①②联立得,k=
,a=1,
∴这条直线的表达式为y=
x+
;
(2)如图所示,
∵k=
,a=1,
∴AB=2,AC=4,BC=2
,C(1,2
),
过点E作EF⊥x轴于点F,
∵△DEC由△ABC旋转而成,
∴CD=AC=4,DE=AB=2,
∵CB⊥AD,
∴AB=BD,
∴D(3,0),∠ADC=∠CAB=60°.
∵∠CDE=∠CAB=60°,
∴∠EDF=60°.
∵∠EDF=∠CDB,∠CBD=∠EFD,
∴△CBD∽△EFD,
∴
=
=
,即
=
=
,解得EF=
,DF=1,
∴OF=1+2+1=4,
∴E(4,1).
 解:(1)设A(-a,0),则B(a,0),直线BC的解析式为x=a,AB=2a,
解:(1)设A(-a,0),则B(a,0),直线BC的解析式为x=a,AB=2a,∵点A在直线y=kx+
| 3 |
∴-ka+
| 3 |
∵∠MAO=60°,
∴BC=ABtan60°=2a×
| 3 |
| 3 |
∴C(a,2
| 3 |
∵点C在直线AC上,
∴ka+
| 3 |
| 3 |
①②联立得,k=
| 3 |
∴这条直线的表达式为y=
| 3 |
| 3 |
(2)如图所示,
∵k=
| 3 |
∴AB=2,AC=4,BC=2
| 3 |
| 3 |
过点E作EF⊥x轴于点F,
∵△DEC由△ABC旋转而成,
∴CD=AC=4,DE=AB=2,
∵CB⊥AD,
∴AB=BD,
∴D(3,0),∠ADC=∠CAB=60°.
∵∠CDE=∠CAB=60°,
∴∠EDF=60°.
∵∠EDF=∠CDB,∠CBD=∠EFD,
∴△CBD∽△EFD,
∴
| DE |
| CD |
| EF |
| BC |
| DF |
| BD |
| 2 |
| 4 |
| EF | ||
2
|
| DF |
| 2 |
| 3 |
∴OF=1+2+1=4,
∴E(4,1).
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
三元一次方程组
的解为( )
|
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下列说法正确的是( )
| A、为了解全市中学生的睡眠状况,宜采用普查方式 |
| B、某地会发生地震是必然事件 |
| C、某校教师150人,其中31岁~35岁组的频率为0.2,那么在该段的教师有30人 |
| D、若甲组数据的方差S甲2=0.1,乙组数据的方差S乙2=0.2,则乙组数据比甲组稳定 |
甲、乙两台机床生产一种零件,在10天中两台机床每天生产的次品数的平均数是
=
=2,方差是:S甲2=1.65,S乙2=0.76,出次品的波动较小的机床是( )
. |
| x甲 |
. |
| 乙 |
| A、甲机床 | B、乙机床 |
| C、甲、乙机床一样 | D、不能确定 |
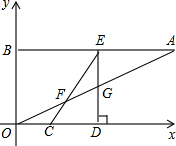 如图,在平面直角坐标系xOy中,点A、B的坐标分别为(16,8)、(0,8),线段CD在x轴上,CD=6,点C从原点出发沿x轴正方向以每秒2个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
如图,在平面直角坐标系xOy中,点A、B的坐标分别为(16,8)、(0,8),线段CD在x轴上,CD=6,点C从原点出发沿x轴正方向以每秒2个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.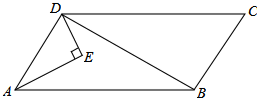 边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED=90°.
边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED=90°.