题目内容
已知三个连续奇数，其中最小的数的平方的三倍减去25和两个较大的数的平方和相等，试求这三个连续奇数．
考点：一元二次方程的应用
专题：数字问题
分析：设3个连续奇数为n，n+2，n+4，根据题意3n2-25=（n+2）2+（n+4）2，解方程得到n，依此即可求解．
解答：解：设3个连续奇数为n，n+2，n+4，依题意有
3n2-25=（n+2）2+（n+4）2，
解得n=15或n=-3，
当n=15时这3个奇数为15，17，19；
当n=-3时这3个奇数为-3，-1，1．
答：这三个连续奇数是15，17，19或-3，-1，1．
3n2-25=（n+2）2+（n+4）2，
解得n=15或n=-3，
当n=15时这3个奇数为15，17，19；
当n=-3时这3个奇数为-3，-1，1．
答：这三个连续奇数是15，17，19或-3，-1，1．
点评：考查一元二次方程的应用；得到连续3个奇数的代数式是解决本题的突破点；关键是得到3个连续奇数的平方的等量关系．
练习册系列答案
相关题目
如果汽车向东行驶3公里记作3公里，向西2公里应记作（ ）
| A、+2公里 | B、-2公里 |
| C、+3公里 | D、-3公里 |
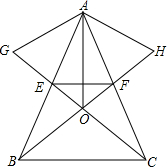如图，在△ABC中，AB=AC，EF∥BC交AB于点E，交AC于点F，分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH，BF、CG交于点O．求证：
以正方形ABCD的AB边为直径作半圆O，过点C作直线切半圆于点F，交AB边于点E，若△CDE的周长为12，则直角梯形ABCE周长为
如图，在△ABC中，AD是BC边上的中线，点E在线段AC上且EC=2AE，线段AD与线段BE交于点F．若△ABC的面积为3，则四边形EFDC的面积为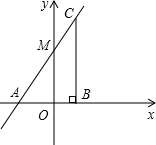
已知：如图，在直角坐标平面中，点A在x轴的负半轴上，直线y=kx+