题目内容
求所有适合于(y-2)x2+yx+2=0的非负整数对(x,y).
考点:非一次不定方程(组)
专题:
分析:首先将原式变形为:(x+1)[xy-2(x-1)]=0,由x是非负整数,可得xy-2(x-1)=0,继而可得x>0,y=2-
,又由x,y是非负整数,即可求得答案.
| 2 |
| x |
解答:解:由题意得:y(x2+x)-2(x2-1)=0,
即:(x+1)[xy-2(x-1)]=0,
∵x≥0,
∴xy-2(x-1)=0,
即:xy=2(x-1),显然x≠0,
∴x>0,y=2-
,
∵x,y是非负整数,
∴x=1或x=2,
当x=1时,y=0,
当x=2时,y=1,
∴只有两组解:
或
,
即适合于(y-2)x2+yx+2=0的非负整数对为:(1,0)或(2,1).
即:(x+1)[xy-2(x-1)]=0,
∵x≥0,
∴xy-2(x-1)=0,
即:xy=2(x-1),显然x≠0,
∴x>0,y=2-
| 2 |
| x |
∵x,y是非负整数,
∴x=1或x=2,
当x=1时,y=0,
当x=2时,y=1,
∴只有两组解:
|
|
即适合于(y-2)x2+yx+2=0的非负整数对为:(1,0)或(2,1).
点评:此题考查了非一次不等式的求解方法.此题难度较大,解题的关键是将原式变形为:(x+1)[xy-2(x-1)]=0,由x,y是非负整数,得到x>0,y=2-
.
| 2 |
| x |

练习册系列答案
相关题目
圆周上共有10个等分点,以其中三点为顶点的直角三角形的个数为( )
| A、20 | B、40 | C、60 | D、80 |
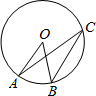 如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=40°,则∠OAC的度数等于( )
如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=40°,则∠OAC的度数等于( )| A、40° | B、60° |
| C、50° | D、20° |
 如图,△ABC中,∠C=90°,∠ABC和∠EAC的平分线交于点D,∠ABD和∠BAD的平分线交于点F,则∠AFB的度数为
如图,△ABC中,∠C=90°,∠ABC和∠EAC的平分线交于点D,∠ABD和∠BAD的平分线交于点F,则∠AFB的度数为