题目内容
用边长单位数大于1的一位数正方形地砖,铺一个矩形的房间,房间的长、宽单位数都是两位数,铺满而无余.已知组成以上三个数目(一位数一个,两位数两个)的五个数码,恰好是五个奇数码1,3,5,7,9,则正方形地砖的边长为 ,矩形房间的长为 ,宽为 .
考点:奇数与偶数
专题:
分析:根据数的整除性特点,分别假设当一位数为1,3,5,7,9进而得出符合要求的答案.
解答:解:由题意得:
∵一位数一个、二位数两个,
∴这两个两位数都是一位数的倍数,
当一位数为1,不符合题意中边长单位数大于1的要求;
当一位数为3,另外4个数为1,5,7,9,合计为22,可以知道不可能组成3的倍数,舍去;
当一位数为5,另外4个数为1,3,7,9,没有5或0,也不可能组成5的倍数;
当一位数为9,另外4个数为1,3,5,7,合计为16,不可能组成3 的倍数,更加不可能是9的倍数;
当一位数为7,另4个数为1,3,5,9,可以发现可以有2个7的倍数35和91
所以正方形的砖的边长7、矩形房间的长91,宽35.
故答案为:7,91,35.
∵一位数一个、二位数两个,
∴这两个两位数都是一位数的倍数,
当一位数为1,不符合题意中边长单位数大于1的要求;
当一位数为3,另外4个数为1,5,7,9,合计为22,可以知道不可能组成3的倍数,舍去;
当一位数为5,另外4个数为1,3,7,9,没有5或0,也不可能组成5的倍数;
当一位数为9,另外4个数为1,3,5,7,合计为16,不可能组成3 的倍数,更加不可能是9的倍数;
当一位数为7,另4个数为1,3,5,9,可以发现可以有2个7的倍数35和91
所以正方形的砖的边长7、矩形房间的长91,宽35.
故答案为:7,91,35.
点评:此题主要考查了数的整除性,根据能整除3,5,9数特点分别进行分析得出符合要求的答案是解题关键.

练习册系列答案
相关题目
已知⊙O1的半径是5cm,⊙O2的半径是2cm,O1O2=3cm,则两圆的位置关系是( )
| A、外离 | B、内切 | C、相交 | D、内含 |
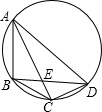 如图,A、B、C、D在同一圆周上,AC与BD交于E,且BC=CD=2,AE=3,则CE的长是
如图,A、B、C、D在同一圆周上,AC与BD交于E,且BC=CD=2,AE=3,则CE的长是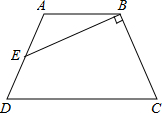 如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是
如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是