题目内容
2.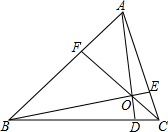 如图.已知△ABC,点E在AC上,点F在AB上,BE与CF交于点O,AD过点O交BC于点D,且AF:BF=1:2.CE:AC=1:4.求BD:DC的值.
如图.已知△ABC,点E在AC上,点F在AB上,BE与CF交于点O,AD过点O交BC于点D,且AF:BF=1:2.CE:AC=1:4.求BD:DC的值.
分析 作EM∥AB交CF于M,作CN∥AB交AD的延长线于N,根据平行线分线段成比例定理得到$\frac{EM}{AF}$=$\frac{CM}{CF}$=$\frac{CE}{CA}$=$\frac{1}{4}$,$\frac{MO}{FO}$=$\frac{EM}{BF}$=$\frac{1}{8}$,$\frac{CN}{AF}$=$\frac{CO}{OF}$=$\frac{1}{2}$,计算得到答案.
解答  解:作EM∥AB交CF于M,作CN∥AB交AD的延长线于N,
解:作EM∥AB交CF于M,作CN∥AB交AD的延长线于N,
∴$\frac{EM}{AF}$=$\frac{CM}{CF}$=$\frac{CE}{CA}$=$\frac{1}{4}$,
∴AF=4EM,CF=4CM,
∴BF=8EM,
∵EM∥AB,
∴$\frac{MO}{FO}$=$\frac{EM}{BF}$=$\frac{1}{8}$,
∴FO=8MO,
∴CM=3OM,
∴FO=2CO,
∵CN∥AB,∴$\frac{CN}{AF}$=$\frac{CO}{OF}$=$\frac{1}{2}$,
∴AF=2CN,BF=4CN,AB=6CN,
∴$\frac{DB}{CD}$=$\frac{AB}{CN}$=$\frac{1}{6}$.
点评 本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.

练习册系列答案
相关题目
8.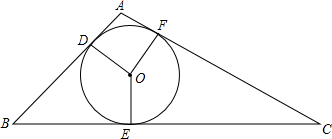 如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
 如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
5.反比例函数y=$\frac{1-2m}{x}$中,当x>0时,y随x的增大而增大,则m的取值范围是( )
| A. | m>$\frac{1}{2}$ | B. | m<2 | C. | m<$\frac{1}{2}$ | D. | m>2 |
 如图,已知AB⊥BC,AD⊥CD.求证:∠A+∠C=180°.
如图,已知AB⊥BC,AD⊥CD.求证:∠A+∠C=180°.