题目内容
15.如果点M在y轴的左侧,且在x轴的上侧,到两坐标轴的距离都是1,则点M的坐标为( )| A. | (-1,2) | B. | (-1,-1) | C. | (-1,1) | D. | (1,1) |
分析 先判断出点M在第二象限,再根据点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
解答 解:∵点M在y轴的左侧,且在x轴的上侧,
∴点M在第二象限,
∵点M到两坐标轴的距离都是1,
∴点M的横坐标为-1,纵坐标为1,
∴点M的坐标为(-1,1).
故选C.
点评 本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.

练习册系列答案
相关题目
5.下列命题正确的是( )
| A. | 有一个角是直角的四边形是矩形 | |
| B. | 对角线垂直的四边形是菱形 | |
| C. | 有一组邻边相等的四边形是菱形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
6.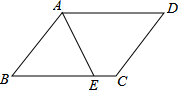 如图,平行四边形ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,平行四边形ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
 如图,平行四边形ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,平行四边形ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
3.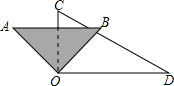 如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )
如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )
 如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )
如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )| A. | ∠AOD>∠BOC | B. | ∠AOC≠∠BOD | C. | ∠AOD-∠BOC=45° | D. | ∠AOD+∠BOC=180° |
20.如果关于x的不等式组$\left\{\begin{array}{l}{x>2}\\{x>m}\end{array}\right.$的解集是x>2,那么m的取值范围是( )
| A. | m≤2 | B. | m≥2 | C. | m≤1 | D. | m>1 |
4.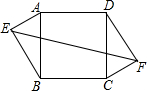 如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
 如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )| A. | 14 | B. | 16 | C. | $14\sqrt{2}$ | D. | $14\sqrt{3}$ |
5. 一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )
 一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )| A. | x<0 | B. | x>0 | C. | x<2 | D. | x>2 |