题目内容
10.已知|a|=3,|b|=2,|c|=1,且a<b<c,求a+b-c的值.分析 由已知中|a|=3,|b|=2,|c|=1,且a<b<c,求出满足条件的a,b,c的值,代入可得答案.
解答 解:∵|a|=3,|b|=2,|c|=1,
∴a=±3,b=±2,c=±1,
又由a<b<c,
故a=-3,b=-2,c=±1,
故a+b-c=-6,或a+b-c=-4.
点评 本题考查的知识点是绝对值的定义,难度不大,解答时要注意a<b<c,对a,b,c值的限制.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
20.下列各式是最简二次根式的是( )
| A. | $\sqrt{{m}^{2}+1}$ | B. | $\sqrt{a{b}^{5}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{3}}$ |
1. 如图,已知直线AB∥直线CD,点E,F分别在直线AB和CD上,EN∥MF,HE∥FN,若∠N=114°,HE平分∠AEN,则∠MFH的度数为( )
如图,已知直线AB∥直线CD,点E,F分别在直线AB和CD上,EN∥MF,HE∥FN,若∠N=114°,HE平分∠AEN,则∠MFH的度数为( )
 如图,已知直线AB∥直线CD,点E,F分别在直线AB和CD上,EN∥MF,HE∥FN,若∠N=114°,HE平分∠AEN,则∠MFH的度数为( )
如图,已知直线AB∥直线CD,点E,F分别在直线AB和CD上,EN∥MF,HE∥FN,若∠N=114°,HE平分∠AEN,则∠MFH的度数为( )| A. | 48° | B. | 58° | C. | 66° | D. | 68° |
15.如果点M在y轴的左侧,且在x轴的上侧,到两坐标轴的距离都是1,则点M的坐标为( )
| A. | (-1,2) | B. | (-1,-1) | C. | (-1,1) | D. | (1,1) |
2.某市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收1.5元(不足1千米按1千米计).某人从甲地到乙地经过的路程是x千米,出租车费为15.5元,那么x的最大值是( )
| A. | 5 | B. | 7 | C. | 8 | D. | 11 |
20.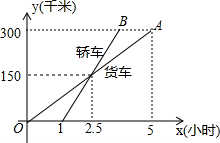 如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
 如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )| A. | 1小时 | B. | 2小时 | C. | 3小时 | D. | 4小时 |
 如图是一个由6个相同的小立方体组成的几何体,从上面看得到的平面图形是( )
如图是一个由6个相同的小立方体组成的几何体,从上面看得到的平面图形是( )


