题目内容
6．
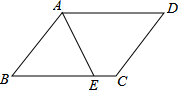如图，平行四边形ABCD的周长为20cm，AE平分∠BAD，若CE=2cm，则AB的长度是（ ）| A． | 10cm | B． | 8cm | C． | 6cm | D． | 4cm |
分析 根据平行四边形的性质得出AB=CD，AD=BC，AD∥BC，推出∠DAE=∠BAE，求出∠BAE=∠AEB，推出AB=BE，设AB=CD=xcm，则AD=BC=（x+2）cm，得出方程x+x+2=10，求出方程的解即可．
解答 解：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，AD∥BC，
∴∠DAE=∠BAE，
∵AE平分∠BAD，
∴∠DAE=∠BAE，
∴∠BAE=∠AEB，
∴AB=BE，
设AB=CD=xcm，则AD=BC=（x+2）cm，
∵?ABCD的周长为20cm，
∴x+x+2=10，
解得：x=4，
即AB=4cm，
故选D．
点评 本题考查了平行四边形的性质，平行线的性质，等腰三角形的判定的应用，解此题的关键是能推出AB=BE，题目比较好，难度适中．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
16．下列计算：（1）34÷35=$\frac{1}{3}$；（2）（$\frac{1}{2012}$）0=（-2012）0；（3）（a-2）5÷（a-5）2=1；（4）x4÷x9=x-5，其中正确的有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
17．
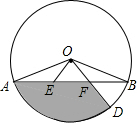如图，AB是⊙O的弦，OA=10，F是线段AB上的点，且FB=FO，OF的延长线交⊙O于点D，∠B=30°，则阴影部分的面积为（ ）
如图，AB是⊙O的弦，OA=10，F是线段AB上的点，且FB=FO，OF的延长线交⊙O于点D，∠B=30°，则阴影部分的面积为（ ）| A． | 25π-$\frac{100\sqrt{3}}{3}$ | B． | 25π-$\frac{50\sqrt{3}}{3}$ | C． | 30π-$\frac{25\sqrt{3}}{2}$ | D． | 20π-$\frac{50\sqrt{3}}{3}$ |
1．
如图，已知直线AB∥直线CD，点E，F分别在直线AB和CD上，EN∥MF，HE∥FN，若∠N=114°，HE平分∠AEN，则∠MFH的度数为（ ）
如图，已知直线AB∥直线CD，点E，F分别在直线AB和CD上，EN∥MF，HE∥FN，若∠N=114°，HE平分∠AEN，则∠MFH的度数为（ ）| A． | 48° | B． | 58° | C． | 66° | D． | 68° |
11．
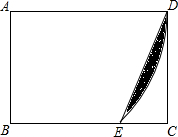在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（ ）
在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（ ）| A． | $\frac{π}{2}$-$\sqrt{2}$ | B． | $\frac{π}{2}$-$\frac{\sqrt{2}}{2}$ | C． | π-$\sqrt{2}$ | D． | π-$\frac{\sqrt{2}}{2}$ |
15．如果点M在y轴的左侧，且在x轴的上侧，到两坐标轴的距离都是1，则点M的坐标为（ ）
| A． | （-1，2） | B． | （-1，-1） | C． | （-1，1） | D． | （1，1） |
16．若a＜b，则下列不等式中成立的是（ ）
| A． | a-b＞0 | B． | a-2＜b-2 | C． | $\frac{1}{2}$a＞$\frac{1}{2}$b | D． | -2a＜-2b |