题目内容
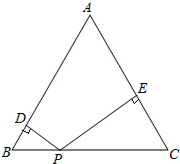 如图所示,等边三角形的高为a,P为BC边上(与BC不重合)的任意一点,且PD⊥AB于点D,PE⊥AC于E,则PE+PD=
如图所示,等边三角形的高为a,P为BC边上(与BC不重合)的任意一点,且PD⊥AB于点D,PE⊥AC于E,则PE+PD=考点:等边三角形的性质
专题:
分析:先设BP=x,则CP=
a-x,根据△ABC是等边三角形,得出∠B=∠C=60°,再利用三角函数求出PD和PE的长,即可得出PE+PD的值.
2
| ||
| 3 |
解答:解:∵BC边上的高线为a,
∴AB=BC=AC=
a,
设BP=x,则CP=
a-x,
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∴PD=sin60°•BP,即PD=
x,
同理可证:PE=
(
a-x)=a-
x,
∴PE+PD=
x+a-
x=a;
故答案为:a.
∴AB=BC=AC=
2
| ||
| 3 |
设BP=x,则CP=
2
| ||
| 3 |
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∴PD=sin60°•BP,即PD=
| ||
| 2 |
同理可证:PE=
| ||
| 2 |
2
| ||
| 3 |
| ||
| 2 |
∴PE+PD=
| ||
| 2 |
| ||
| 2 |
故答案为:a.
点评:此题主要考查了等边三角形的性质,用到的知识点是三角函数,难度不大,有利于培养同学们钻研和探索问题的精神.

练习册系列答案
相关题目
 如图,已知线段AB.
如图,已知线段AB.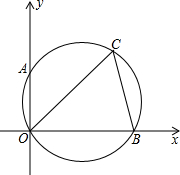 如图,在平面直角坐标系中,△OBC的外接圆交y轴于点A(0,2),∠OCB=60°,∠COB=45°.求点C的坐标.
如图,在平面直角坐标系中,△OBC的外接圆交y轴于点A(0,2),∠OCB=60°,∠COB=45°.求点C的坐标. 如图,△ABC沿DE折叠后,点A落在BC边上的点A′处,且DE∥BC,∠B=50°,则∠BDA′=
如图,△ABC沿DE折叠后,点A落在BC边上的点A′处,且DE∥BC,∠B=50°,则∠BDA′=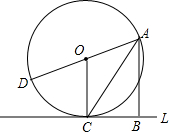 如图所示,直线L切⊙O于点C,AD为⊙O的任意一条直径,点B在直线L上,且∠BAC=∠CAD(AD与AB不在一条直线上),试判断四边形ABCO为怎样的特殊四边形?
如图所示,直线L切⊙O于点C,AD为⊙O的任意一条直径,点B在直线L上,且∠BAC=∠CAD(AD与AB不在一条直线上),试判断四边形ABCO为怎样的特殊四边形? 如图所示,是一条高速公路的隧道口在平面直角坐标系上的示意图,点A 和A1、点B和B1分别关于y轴对称,隧道拱部分BCB1为一条抛物线,最高点C离路面AA1的距离为8m,点B离路面为6m,隧道的宽度AA1为16m;
如图所示,是一条高速公路的隧道口在平面直角坐标系上的示意图,点A 和A1、点B和B1分别关于y轴对称,隧道拱部分BCB1为一条抛物线,最高点C离路面AA1的距离为8m,点B离路面为6m,隧道的宽度AA1为16m;