题目内容
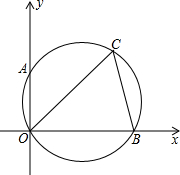 如图,在平面直角坐标系中,△OBC的外接圆交y轴于点A(0,2),∠OCB=60°,∠COB=45°.求点C的坐标.
如图,在平面直角坐标系中,△OBC的外接圆交y轴于点A(0,2),∠OCB=60°,∠COB=45°.求点C的坐标.考点:圆周角定理,坐标与图形性质,解直角三角形
专题:计算题
分析:作CH⊥OB,连结AB,如图,易得△OCH为等腰直角三角形,则OH=CH,再根据圆周角定理,由∠AOB=90°得AB为△OBC的外接圆⊙D的直径,连结CD,得到∠OAB=∠OCB=60°,
所以∠ABO=30°,可计算出AB=2OA=4,OB=
OA=2
,接着判断△CBD为等腰直角三角形,得到BC=
BD=2
,设OH=x,则CH=x,BH=2
-x,然后在Rt△BCH中,根据勾股定理得到(2
-x)2+x2=(2
)2,再解方程求出x即可得到C点坐标.
所以∠ABO=30°,可计算出AB=2OA=4,OB=
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
解答:解:作CH⊥OB,连结AB,如图,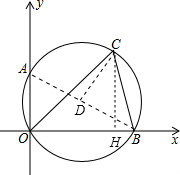
∵∠COB=45°,
∴△OCH为等腰直角三角形,
∴OH=CH,
∵∠AOB=90°,
∴AB为△OBC的外接圆⊙D的直径,
连结CD,
∵∠OAB=∠OCB=60°,
∴∠ABO=30°,
∴AB=2OA=4,
OB=
OA=2
,
∵∠CDB=2∠COB=90°,
∴△CBD为等腰直角三角形,
∴BC=
BD=2
,
设OH=x,则CH=x,BH=2
-x,
在Rt△BCH中,
∵BH2+CH2=BC2,
∴(2
-x)2+x2=(2
)2,解得x1=
+1,x2=
-1(舍去),
∴C点坐标为(
+1,
+1).

∵∠COB=45°,
∴△OCH为等腰直角三角形,
∴OH=CH,
∵∠AOB=90°,
∴AB为△OBC的外接圆⊙D的直径,
连结CD,
∵∠OAB=∠OCB=60°,
∴∠ABO=30°,
∴AB=2OA=4,
OB=
| 3 |
| 3 |
∵∠CDB=2∠COB=90°,
∴△CBD为等腰直角三角形,
∴BC=
| 2 |
| 2 |
设OH=x,则CH=x,BH=2
| 3 |
在Rt△BCH中,
∵BH2+CH2=BC2,
∴(2
| 3 |
| 2 |
| 3 |
| 3 |
∴C点坐标为(
| 3 |
| 3 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了坐标与图形性质.

练习册系列答案
相关题目
截止到4月25日,雅安三个重灾县的直接经济损失已经达到了上年GDP总和的21倍,已知上年GDP总和约为80亿元,则三个重灾县的直接经济损失用科学记数法表示约为( )
| A、1680亿元 |
| B、1.68×1011元 |
| C、1.68×1012元 |
| D、0.168×1012元 |
 如图,AD、BC交于点O,P为AB、CD延长线的交点,且PA•PB=PC•PD.试说明:△PAD∽△PCB.
如图,AD、BC交于点O,P为AB、CD延长线的交点,且PA•PB=PC•PD.试说明:△PAD∽△PCB. 已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.
已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.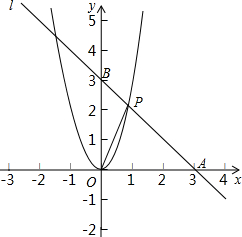 如图,直线l过A(3,0)和B(0,3)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若△AOP的面积为3,求二次函数的表达式.
如图,直线l过A(3,0)和B(0,3)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若△AOP的面积为3,求二次函数的表达式.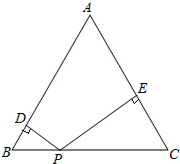 如图所示,等边三角形的高为a,P为BC边上(与BC不重合)的任意一点,且PD⊥AB于点D,PE⊥AC于E,则PE+PD=
如图所示,等边三角形的高为a,P为BC边上(与BC不重合)的任意一点,且PD⊥AB于点D,PE⊥AC于E,则PE+PD=