题目内容
18．
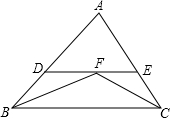如图，在△BAC中，∠B和∠C的平分线相交于点F，过点F作DE∥BC交AB于点D，交AC于点E，若BD=5，CE=4，则线段DE的长为（ ）| A． | 9 | B． | 6 | C． | 5 | D． | 4 |
分析 根据△ABC中，∠ABC和∠ACB的平分线相交于点F．求证∠DBF=∠FBC，∠ECF=∠BCF，再利用两直线平行内错角相等，求证出∠DFB=∠DBF，∠CFE=∠BCF，即BD=DF，FE=CE，然后利用等量代换即可求出线段DE的长．
解答 解：∵∠ABC和∠ACB的平分线相交于点F，
∴∠DBF=∠FBC，∠ECF=∠BCF，
∵DE∥BC，交AB于点D，交AC于点E，
∴∠DFB=∠DBF，∠CFE=∠ECF，
∴BD=DF=5，FE=CE=4，
∴DE=DF+CE=5+4=9．
故选A．
点评 本题主要考查了学生对等腰三角形的判定与性质和平行线段性质的理解和掌握，此题难度不大，是一道基础题．
练习册系列答案
相关题目
如图，在△ABC中，∠C=90°，sinA=$\frac{2}{5}$，D为AC上一点，∠BDC=45°，DC=6，求AD的长．
13．下列命题中，逆命题不成立的是（ ）
| A． | 若x2=y2，则x=y | |
| B． | 若x，y互为倒数，则xy=1 | |
| C． | 线段垂直平分线上的点到线段的两个端点的距离相等 | |
| D． | 全等三角形的对应角相等 |
如图，四边形ABCD的对角线AC和BD相交于点E，如果△CDE的面积为3，△BCE的面积为4，△AED的面积为6，那么△ABE的面积为8．
如图，△ABC中，D点在BC上，现有下列四个命题：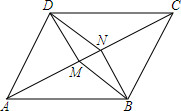
如图：已知?ABCD中，DM⊥AC于M，BN⊥AC于N，求证：四边形DMBN为平行四边形．