题目内容
3．
如图，四边形ABCD的对角线AC和BD相交于点E，如果△CDE的面积为3，△BCE的面积为4，△AED的面积为6，那么△ABE的面积为8．
分析 根据三角形的高相等，面积比等于底的比，可得CE：AE=$\frac{1}{2}$，进而可求出答案．
解答 解：∵S△CDE=3，S△ADE=6，
∴CE：AE=3：6=$\frac{1}{2}$（高相等，面积比等于底的比）
∴S△BCE：S△ABE=CE：AE=$\frac{1}{2}$，
∵S△BCE=4，
∴S△ABE=8．
故答案为：8．
点评 本题考查了三角形的面积，弄清题中各个三角形之间面积的关系是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
13．
如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG．DE，FG，$\widehat{AC}$，$\widehat{BC}$的中点分别是M，N，P，Q．若MP+NQ=12，AC+BC=16，则AB的长为（ ）
如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG．DE，FG，$\widehat{AC}$，$\widehat{BC}$的中点分别是M，N，P，Q．若MP+NQ=12，AC+BC=16，则AB的长为（ ）| A． | 9$\sqrt{2}$ | B． | $\frac{90}{7}$ | C． | 12 | D． | 16 |
如图，A、B两村和一条小河，要在河边L建一水厂Q向两村供水，若要使自来水厂到两村的输水管用料最省，厂址Q应选在哪个位置？请将上述情况下的自来水厂厂址标出，并保留作图痕迹．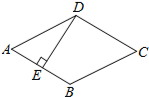
如图，菱形ABCD中，E是AB中点，DE⊥AB，则∠ADC的度数为120°．
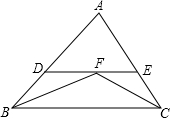如图，在△BAC中，∠B和∠C的平分线相交于点F，过点F作DE∥BC交AB于点D，交AC于点E，若BD=5，CE=4，则线段DE的长为（ ）
如图，梯形ABCD中，DC∥EF∥AB，AC交EF于G．若AE=2ED，CF=2cm，那么CB的长是多少？