题目内容
8．
如图，在△ABC中，∠C=90°，sinA=$\frac{2}{5}$，D为AC上一点，∠BDC=45°，DC=6，求AD的长．
分析 根据已知条件求出BC=DC=6，再根据正弦的定义求出AB，再根据勾股定理求出AC，最后根据AD=AC-DC求出AD的长．
解答 解：∵∠C=90°，∠BDC=45°，
∴∠DBC=45°，
∵DC=6，
∴BC=6，
∵sinA=$\frac{2}{5}$，
∴AB=15，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{5}^{2}-{6}^{2}}$=3$\sqrt{21}$，
∴AD=AC-DC=3$\sqrt{21}$-6．
点评 此题考查了解直角三角形，用到的知识点是直角三角形的性质、正弦的定义、勾股定理，关键是根据题意求出AB的长．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知网格上最小的正方形的边长为1．
已知：∠α．
13．
如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG．DE，FG，$\widehat{AC}$，$\widehat{BC}$的中点分别是M，N，P，Q．若MP+NQ=12，AC+BC=16，则AB的长为（ ）
如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG．DE，FG，$\widehat{AC}$，$\widehat{BC}$的中点分别是M，N，P，Q．若MP+NQ=12，AC+BC=16，则AB的长为（ ）| A． | 9$\sqrt{2}$ | B． | $\frac{90}{7}$ | C． | 12 | D． | 16 |
如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．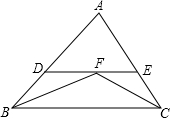
如图，在△BAC中，∠B和∠C的平分线相交于点F，过点F作DE∥BC交AB于点D，交AC于点E，若BD=5，CE=4，则线段DE的长为（ ）