题目内容
13.先化简,再求值:$\frac{a-b}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$),其中a=$\frac{\sqrt{3}}{2}$$+\frac{1}{5}$,b=$\frac{\sqrt{3}}{2}$$-\frac{1}{5}$.分析 将原式根据分式的混合运算顺序和法则化简后,把a、b的值代入计算可得.
解答 解:原式=$\frac{a-b}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$,
当a=$\frac{\sqrt{3}}{2}$$+\frac{1}{5}$,b=$\frac{\sqrt{3}}{2}$$-\frac{1}{5}$时,
原式=$\frac{1}{\frac{\sqrt{3}}{2}+\frac{1}{5}-(\frac{\sqrt{3}}{2}-\frac{1}{5})}$=$\frac{5}{2}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
相关题目
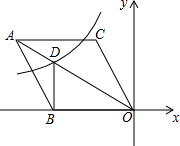 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,3$\sqrt{3}}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是-12$\sqrt{3}$.
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,3$\sqrt{3}}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是-12$\sqrt{3}$. 已知,如图,在?ABCD中,AB=5cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=2cm.
已知,如图,在?ABCD中,AB=5cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=2cm.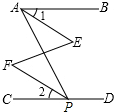 如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数.
如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数. 已知反比例函数y=$\frac{k}{x}$的图象经过点(-3,4).
已知反比例函数y=$\frac{k}{x}$的图象经过点(-3,4).