题目内容
4.(1)化简:$\sqrt{8}$+3$\sqrt{\frac{1}{3}}$-$\frac{1}{\sqrt{2}}$+$\frac{\sqrt{3}}{2}$(2)解分式方程:$\frac{3}{x-1}$-$\frac{x+2}{{x}^{2}-x}$=0.
分析 (1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)先把分式方程化为整式方程,解整式方程得到x=1,然后进行检验确定分式方程的解.
解答 解:(1)原式=2$\sqrt{2}$+$\sqrt{3}$-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$
=$\frac{3\sqrt{2}}{2}$+$\frac{3\sqrt{3}}{2}$;
(2)方程两边乘以x(x-1)得3x-(x+2)=0,
解得x=1,
检验:当x=1时,x(x-1)=0,所以x=1是原方程的增根,
所以原方程没有实数解.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.也考查了解分式方程.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
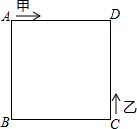 如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若甲的速度是乙的速度的3倍,则它们第2017次相遇在边CD上.
如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若甲的速度是乙的速度的3倍,则它们第2017次相遇在边CD上.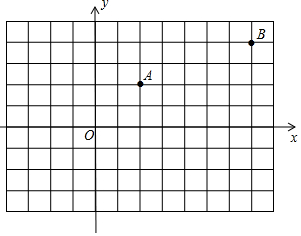 如图,已知A,B两村庄的坐标分别为(2,2),(7,4),一辆汽车从O点出发,在x轴上行驶.
如图,已知A,B两村庄的坐标分别为(2,2),(7,4),一辆汽车从O点出发,在x轴上行驶.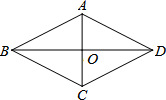 如图,菱形ABCD中,对角线AC、BD相交于点O.AC=3$\sqrt{2}$+2$\sqrt{3}$,BD=3$\sqrt{2}$-2$\sqrt{3}$.求:菱形ABCD的面积和周长.
如图,菱形ABCD中,对角线AC、BD相交于点O.AC=3$\sqrt{2}$+2$\sqrt{3}$,BD=3$\sqrt{2}$-2$\sqrt{3}$.求:菱形ABCD的面积和周长.