题目内容
8．已知两直线l1：y=k1x+b1，l2：y=k2x+b2，若l1⊥l2，则有k1•k2=-1，若直线经过A（2，3），且与y=-$\frac{1}{3}$x+3垂直，求该直线的表达式．分析 根据直线互相垂直，则k1•k2=-1，可得出过点A直线的k等于3，得出所求的解析式即可．
解答 解：∵过点A直线与y=-$\frac{1}{3}$x+3垂直，
∴设过点A直线的直线解析式为y=3x+b，
把A（2，3）代入得，b=-3，
∴解析式为y=3x-3．
点评 本题考查了两直线相交或平行问题，关键是掌握当两直线垂直时，两个k值的乘积为-1．
练习册系列答案
阅读快车系列答案
相关题目
18．
如图，经过原点O的⊙P与x、y轴分别交于A、B两点，点C是劣弧$\widehat{OB}$上一点，则∠ACB=（ ）
如图，经过原点O的⊙P与x、y轴分别交于A、B两点，点C是劣弧$\widehat{OB}$上一点，则∠ACB=（ ）| A． | 80° | B． | 90° | C． | 100° | D． | 无法确定 |
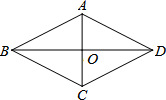如图，菱形ABCD中，对角线AC、BD相交于点O．AC=3$\sqrt{2}$+2$\sqrt{3}$，BD=3$\sqrt{2}$-2$\sqrt{3}$．求：菱形ABCD的面积和周长．
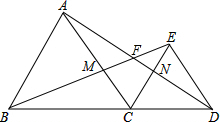如图，B、C、D在同一直线上，△ABC和△DCE都是等边三角形，且在直线BD的同侧，BE交AD于F，BE交AC于M，AD交CE于N．