题目内容
8．已知抛物线y=（a+1）x2+2x+a2-a-2（a为常数）经过原点，则a=2．分析 根据抛物线过原点得出a2-a-2=0，求得a，由a+1≠0，得出a的值即可．
解答 解：∵抛物线y=（a+1）x2+2x+a2-a-2（a为常数）经过原点，
∴a2-a-2=0，
解得a=2或-1，
∵a+1≠0，
∴a≠-1，
∴a=2，
故答案为2．
点评 本题考查了二次函数图象上点的坐标特征，利用了抛物线过原点得出a的值是解题的关键．
练习册系列答案
相关题目
解这个不等式组，并将解集在数轴上表示出来：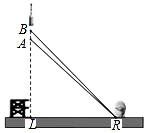
2016年2月1日，我国在西昌卫星发射中心，用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道，如图，火箭从地面L处发射，当火箭到达A点时，从位于地面R处雷达站测得AR的距离是6km，仰角为42.4°；1秒后火箭到达B点，此时测得仰角为45.5°
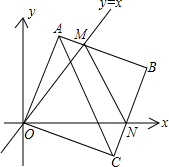如图①，在平面直角坐标中，边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，O为坐标原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N．
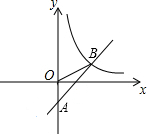如图，在平面直角坐标系中，直线AB与y轴相交于点A（0，-2），与反比例函数在第一象限内的图象相交于点B（m，2），△AOB的面积为4．