题目内容
12. 解这个不等式组,并将解集在数轴上表示出来:
解这个不等式组,并将解集在数轴上表示出来:$\left\{\begin{array}{l}{2x-2<3x①}\\{\frac{x+2}{5}-\frac{x+1}{4}≥0②}\end{array}\right.$.
分析 首先分别解出两个不等式的解集,再根据解集的规律:大小小大中间找确定不等式组的解集.
解答 解:解不等式①得:x>-2,
解不等式②得:x≤3,
∴该不等式组的解集为:-2<x≤3.
在数轴上表示: .
.
点评 此题主要考查了一元一次不等式组的解法,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
7.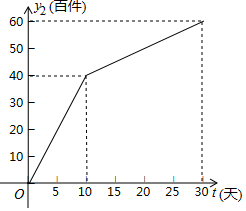 我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
 我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量 y1(百件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
4.下列各组数中互为相反数的是( )
| A. | -2与-$\frac{1}{2}$ | B. | 2与|-2| | C. | -2与$\root{3}{-8}$ | D. | -2与$\sqrt{(-2)^{2}}$ |
1. 某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
各年级学生成绩统计表
根据以上信息,解决下列问题:
(1)在统计表中,a的值为24,b的值为7;
(2)在扇形统计图中,八年级所对应的扇形圆心角为108°;
(3)若该校三个年级共2000名学生参加考试,试估计其中体育成绩不合格的人数.
 某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:各年级学生成绩统计表
| 各年级学生成绩统计表 | ||||
| 优秀 | 良好 | 合格 | 不合格 | |
| 七年级 | 28 | 20 | a | 8 |
| 八年级 | 29 | 13 | 13 | 5 |
| 九年级 | 24 | 15 | 14 | b |
(1)在统计表中,a的值为24,b的值为7;
(2)在扇形统计图中,八年级所对应的扇形圆心角为108°;
(3)若该校三个年级共2000名学生参加考试,试估计其中体育成绩不合格的人数.
 如图所示,将一块含30°角的直角三角板ABC绕点A旋转到三角形AED的位置,使得C、A、E三点在同一直线上,则旋转角是150度.
如图所示,将一块含30°角的直角三角板ABC绕点A旋转到三角形AED的位置,使得C、A、E三点在同一直线上,则旋转角是150度.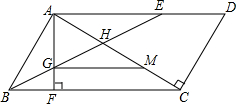 已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.
已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.