题目内容
16.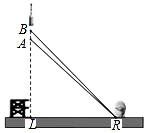 2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°
2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°(1)求发射台与雷达站之间的距离LR;
(2)求这枚火箭从A到B的平均速度.(结果保留两位小数)
【参考数据:sin42.4°≈0.674,cos42.4°≈0.738,tan42.4°≈0.913,sin45.5°≈0.713,cos45.5°≈0.701,tan45.5°≈1.018】
分析 (1)根据题意直接利用锐角三角函数关系得出LR=AR•cos∠ARL求出答案即可;
(2)根据题意直接利用锐角三角函数关系得出BL=LR•tan∠BRL,再利用AL=ARsin∠ARL,求出AB的值,进而得出答案.
解答 解:(1)在Rt△ALR中,AR=6km,∠ARL=42.4°,
由cos∠ARL=$\frac{RL}{AR}$,得LR=AR•cos∠ARL=6×cos42.4°=6×0.378≈4.43(km).
答:发射台与雷达站之间的距离LR为4.43km;
(2)在Rt△BLR中,LR=4.44km,∠BRL=45.5°,
由tan∠BRL=$\frac{BL}{LR}$,得BL=LR•tan∠BRL=4.43×tan45.5°≈4.43×1.018≈4.510(km),
又∵sin∠ARL=$\frac{AL}{AR}$,得AL=ARsin∠ARL=6×sin42.4°=6×0.674≈4.044km),
∴AB=BL-AL=4.510-4.044=0.466≈0.47(km),
0.47÷1=0.47(km\s)
答:这枚火箭从A到B的平均速度大约是0.47km/s.
点评 本题主要考查了解直角三角形的应用,正确选择锐角三角函数关系是解题关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
1. 某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
各年级学生成绩统计表
根据以上信息,解决下列问题:
(1)在统计表中,a的值为24,b的值为7;
(2)在扇形统计图中,八年级所对应的扇形圆心角为108°;
(3)若该校三个年级共2000名学生参加考试,试估计其中体育成绩不合格的人数.
 某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:各年级学生成绩统计表
| 各年级学生成绩统计表 | ||||
| 优秀 | 良好 | 合格 | 不合格 | |
| 七年级 | 28 | 20 | a | 8 |
| 八年级 | 29 | 13 | 13 | 5 |
| 九年级 | 24 | 15 | 14 | b |
(1)在统计表中,a的值为24,b的值为7;
(2)在扇形统计图中,八年级所对应的扇形圆心角为108°;
(3)若该校三个年级共2000名学生参加考试,试估计其中体育成绩不合格的人数.
11.将函数y=-3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
| A. | y=-3x+2 | B. | y=-3x-2 | C. | y=-3(x+2) | D. | y=-3(x-2) |
6.已知点P(1,3),将线段OP绕原点O按顺时针方向旋转90°得到线段OP′,则点P′的坐标是( )
| A. | (-1,3) | B. | (1,-3) | C. | (3,-1) | D. | (3,1) |