题目内容
9.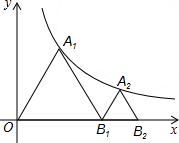 如图,点A1,A2依次在y=$\frac{9\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上.若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为(6$\sqrt{2}$,0).
如图,点A1,A2依次在y=$\frac{9\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上.若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为(6$\sqrt{2}$,0).
分析 由于△A1OB1等边三角形,作A1C⊥OB1,垂足为C,由等边三角形的性质求出A1C=$\sqrt{3}$OC,设A1的坐标为(m,$\sqrt{3}$m),根据点A1是反比例函数y=$\frac{9\sqrt{3}}{x}$(x>0)的图象上的一点,求出BO的长度;作A2D⊥B1B2,垂足为D.设B1D=a,由于,△A2B1B2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点A2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出B2点的坐标.
解答 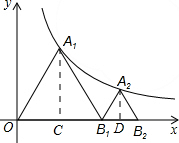 解:作A1C⊥OB1,垂足为C,
解:作A1C⊥OB1,垂足为C,
∵△A1OB1为等边三角形,
∴∠A1OB1=60°,
∴tan60°=$\frac{{A}_{1}C}{OC}$=$\sqrt{3}$,
∴A1C=$\sqrt{3}$OC,
设A1的坐标为(m,$\sqrt{3}$m),
∵点A1在y=$\frac{9\sqrt{3}}{x}$(x>0)的图象上,
∴m$•\sqrt{3}m$=9$\sqrt{3}$,解得m=3,
∴OC=3,
∴OB1=6,
作A2D⊥B1B2,垂足为D.
设B1D=a,
则OD=6+a,A2D=$\sqrt{3}$a,
∴A2(6+a,$\sqrt{3}$a).
∵A2(6+a,$\sqrt{3}$a)在反比例函数的图象上,
∴代入y=$\frac{9\sqrt{3}}{x}$,得(6+a)•$\sqrt{3}$a=9$\sqrt{3}$,
化简得a2+6a-9=0
解得:a=-3±3$\sqrt{2}$.
∵a>0,
∴a=-3+3$\sqrt{2}$.
∴B1B2=-6+6$\sqrt{2}$,
∴OB2=OB1+B1B2=6$\sqrt{2}$,
所以点B2的坐标为(6$\sqrt{2}$,0).
故答案是:(6$\sqrt{2}$,0).
点评 此题综合考查了反比例函数的性质,反比例函数图象上点的坐标特征,正三角形的性质等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

 如图所示的三视图所对应的几何体是( )
如图所示的三视图所对应的几何体是( )| A. |  | B. |  | C. |  | D. |  |
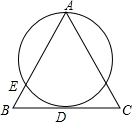 如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )| A. | 线段AE的中垂线与线段AC的中垂线的交点 | |
| B. | 线段AB的中垂线与线段AC的中垂线的交点 | |
| C. | 线段AE的中垂线与线段BC的中垂线的交点 | |
| D. | 线段AB的中垂线与线段BC的中垂线的交点 |
| 类别 | 彩电 | 冰箱 | 洗衣机 |
| 进价(元/台) | 2000 | 1600 | 1000 |
| 售价(元/台) | 2300 | 1800 | 1100 |
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
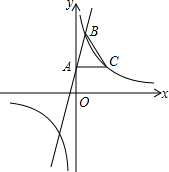 如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=$\frac{k}{x}$(k≠0)的图象于点C,连接BC.
如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=$\frac{k}{x}$(k≠0)的图象于点C,连接BC. 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图: 如图,一条公路的转弯处是一段圆弧($\widehat{AB}$).
如图,一条公路的转弯处是一段圆弧($\widehat{AB}$).