题目内容
1. 如图,一条公路的转弯处是一段圆弧($\widehat{AB}$).
如图,一条公路的转弯处是一段圆弧($\widehat{AB}$).(1)用直尺和圆规作出$\widehat{AB}$所在圆的圆心O;(要求保留作图痕迹,不写作法)
(2)若$\widehat{AB}$的中点C到弦AB的距离为20m,AB=80m,求$\widehat{AB}$所在圆的半径.
分析 (1)连结AC、BC,分别作AC和BC的垂直平分线,两垂直平分线的交点为点O,如图1;
(2)连接OA,OC,OC交AB于D,如图2,根据垂径定理的推论,由C为$\widehat{AB}$的中点得到OC⊥AB,AD=BD=$\frac{1}{2}$AB=40,则CD=20,设⊙O的半径为r,在Rt△OAD中利用勾股定理得到r2=(r-20)2+402,然后解方程即可.
解答 解:(1)如图1,
点O为所求;
(2)连接OA,OC,OC交AB于D,如图2,
∵C为$\widehat{AB}$的中点,
∴OC⊥AB,
∴AD=BD=$\frac{1}{2}$AB=40,
设⊙O的半径为r,则OA=r,OD=OD-CD=r-20,
在Rt△OAD中,∵OA2=OD2+AD2,
∴r2=(r-20)2+402,解得r=50,
即$\widehat{AB}$所在圆的半径是50m.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法;解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了勾股定理和垂径定理.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
11. 如图是由4个大小相等的正方形搭成的几何体,其左视图是( )
如图是由4个大小相等的正方形搭成的几何体,其左视图是( )
 如图是由4个大小相等的正方形搭成的几何体,其左视图是( )
如图是由4个大小相等的正方形搭成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
12.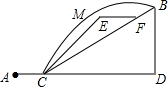 如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
 如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )| A. | A→C→D→B | B. | A→C→F→B | C. | A→C→E→F→B | D. | A→C→M→B |
6.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | 3ab-ab=2ab | C. | a(a2-a)=a2 | D. | $\root{3}{8}=2\sqrt{2}$ |
10.在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
11.-5的绝对值是( )
| A. | -5 | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | 5 |
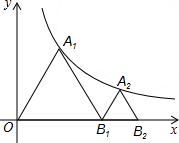 如图,点A1,A2依次在y=$\frac{9\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上.若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为(6$\sqrt{2}$,0).
如图,点A1,A2依次在y=$\frac{9\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上.若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为(6$\sqrt{2}$,0). 如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求$\frac{DE}{BC}$的值.
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求$\frac{DE}{BC}$的值. 如图,在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件AB=CD,使△ABD≌△CDB.(只需写一个)
如图,在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件AB=CD,使△ABD≌△CDB.(只需写一个)