题目内容
20.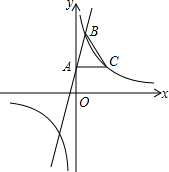 如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=$\frac{k}{x}$(k≠0)的图象于点C,连接BC.
如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=$\frac{k}{x}$(k≠0)的图象于点C,连接BC.(1)求反比例函数的表达式.
(2)求△ABC的面积.
分析 (1)先由一次函数y=3x+2的图象过点B,且点B的横坐标为1,将x=1代入y=3x+2,求出y的值,得到点B的坐标,再将B点坐标代入y=$\frac{k}{x}$,利用待定系数法即可求出反比例函数的表达式;
(2)先由一次函数y=3x+2的图象与y轴交于点A,求出点A的坐标为(0,2),再将y=2代入y=$\frac{5}{x}$,求出x的值,那么AC=$\frac{5}{2}$.过B作BD⊥AC于D,则BD=yB-yC=5-2=3,然后根据S△ABC=$\frac{1}{2}$AC•BD,将数值代入计算即可求解.
解答 解:(1)∵一次函数y=3x+2的图象过点B,且点B的横坐标为1,
∴y=3×1+2=5,
∴点B的坐标为(1,5).
∵点B在反比例函数y=$\frac{k}{x}$的图象上,
∴k=1×5=5,
∴反比例函数的表达式为y=$\frac{5}{x}$;
(2)∵一次函数y=3x+2的图象与y轴交于点A,
∴当x=0时,y=2,
∴点A的坐标为(0,2),
∵AC⊥y轴,
∴点C的纵坐标与点A的纵坐标相同,是2,
∵点C在反比例函数y=$\frac{5}{x}$的图象上,
∴当y=2时,2=$\frac{5}{x}$,解得x=$\frac{5}{2}$,
∴AC=$\frac{5}{2}$.
过B作BD⊥AC于D,则BD=yB-yC=5-2=3,
∴S△ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×$\frac{5}{2}$×3=$\frac{15}{4}$.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,平行于y轴的直线上点的坐标特征,三角形的面积,难度适中.求出反比例函数的解析式是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图是由4个大小相等的正方形搭成的几何体,其左视图是( )
如图是由4个大小相等的正方形搭成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
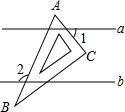 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ③④ |
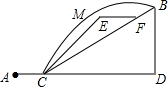 如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )| A. | A→C→D→B | B. | A→C→F→B | C. | A→C→E→F→B | D. | A→C→M→B |
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
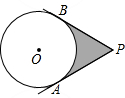 如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,PA=$\sqrt{3}$,∠P=60°,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}$π.
如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,PA=$\sqrt{3}$,∠P=60°,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}$π.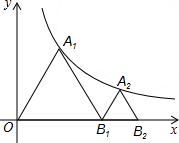 如图,点A1,A2依次在y=$\frac{9\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上.若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为(6$\sqrt{2}$,0).
如图,点A1,A2依次在y=$\frac{9\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上.若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为(6$\sqrt{2}$,0).