题目内容
将二次函数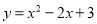
化为
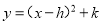的形式，结果为（ ）
A.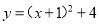 
B.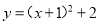 
C. 
D. 
D
【解析】
故选：D．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
相关题目
下列函数中属于一次函数的是( )，属于反比例函数的是( )，属于二次函数的是( )
A. y＝x(x＋1) B. xy＝1
C. y＝2x2－2(x＋1)2 D.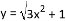 
CBA
【解析】根据题意可知y=x（x+1）=x2+x，可由二次函数的定义，可知是二次函数；根据xy=1是反比例关系，所以是反比例函数；而y＝2x2－2(x＋1)2= y＝2x2－2(x2+2x+1)=-4x-2，是一次函数；函数是带二次根号的函数.
故答案为：C、B、A. 已知m，n是关于x的方程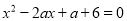
的两实根，求
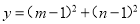的最小值．
8
【解析】试题分析：根据方程有两个根，利用根的判别式求出a的取值范围，再根据根与系数的关系求出m+n与mn的值，然后把整理成m+n与mn的形式，代入进行计算求解．
试题解析：依题意△=≥0，
即，
∴a≤-2或a≥3，
由m+n=2a，mn=a+6，
即
=
=
=，
∴a=3时，y的最小值为8．
故答案为：8． 如图图形中，阴影部分面积相等的是（ ）
A. 甲 乙
B. 甲 丙
C. 乙 丙
D. 丙 丁
B
【解析】根据题意，可知：
甲：直线与x轴交点为（3，0），与y轴的交点为（0，4），则阴影部分的面积为×3×4=6；
乙：阴影部分为斜边为4的等腰直角三角形，其面积为×4×2=4；
丙：抛物线与x轴的两个交点为（-3，0）与（3，0），顶点坐标为（0，-2），则阴影部分的面积为×6×2=6；
丁：此函数是反比例函数，那么阴影部分的面积为×6=3；
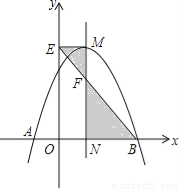
因此甲、丙... 如图，抛物线
与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.
（1），（1，4）；（2）.
【解析】试题分析：（1）直接将（﹣1，0）代入求出即可，再利用配方法求出顶点坐标.
（2）利用EM∥BN，则△EMF∽△BNF，进而求出△EMF与△BNE的面积之比．
试题解析：【解析】
（1）∵点A在抛物线上，
∴，解得：c=3，
∴抛物线的解析式为.
∵，
∴抛物线的顶点M（1，4）；
（2）∵A（﹣1，0），抛物... 二次函数y=-x2+bx+c的图象的最高点是(-1，-3)，则b，c的值分别是( )
A. b=2，c=4 B. b=2，c=-4 C. b=-2，c=4 D. b=-2，c=-4
D
【解析】试题分析：由题可得函数顶点坐标是（-1，-3）所以对称轴是x=-1,对称轴x=,a=-1,所以b=-2,将点（-1，-3）代入表达式得c=-4,所以函数表达式为y=-x2-2x-4,故b=-2,c=-4,故选D. 用一根长为80cm的铁丝，把它弯成一个矩形，设矩形的面积为ycm2，一边长为xcm，则y与x的函数表达式为___________（化为一般式）
【解析】由题意得：矩形的另一边长=80÷2-x=40-x，
∴y=x（40-x）=．
故答案为：． 如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3，那么c的值等于（ ）
A. 8
B. 14
C. 8或14
D. -8或-14
C
【解析】根据题意，得
，
解得c=8或14．
故选：C． 如图，在一笔直的海岸线l上有A、B两个码头，A在B的正东方向，一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处，此时从B码头测得小船在它的北偏东45°的方向．求此时小船到B码头的距离（即BP的长）和A、B两个码头间的距离（结果都保留根号）．
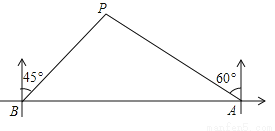
小船到B码头的距离是10海里，A、B两个码头间的距离是（10+10）海里
【解析】试题分析：过P作PM⊥AB于M，求出∠PBM=45°，∠PAM=30°，求出PM，即可求出BM、AM、BP．
试题解析：如图：过P作PM⊥AB于M，则∠PMB=∠PMA=90°，∵∠PBM=90°﹣45°=45°，∠PAM=90°﹣60°=30°，AP=20，∴PM=AP=10，AM=PM=，∴∠BPM=...