题目内容
12.如图,已知∠ABC=40°,射线DE与AB相交于点O,且DE∥BC.解答以下问题:(注∠EDF为小于180°的角)(1)画∠EDF,使∠DF的另一边DF∥AB.请在如图①和图②中画出符合题意的图形,并求∠EDF的度数.(2)如果∠EDF的顶点D在∠ABC的内部,边DE∥BC,另一边DF∥AB.请在如图③和图④中画出相应的图形,并使用量角器分别测量出∠ABC与∠EDF的度数后,直接写出∠ABC与∠EDF的关系,不必说明理由∠ABC+∠EDF=180°或∠ABC=∠EDF.
(3)如果∠EDF的顶点D在∠ABC的内部,边DF⊥BC,请在如图⑤中画出相应的图形,并使用量角器分别测量出∠ABC与∠EDF的度数后,直接写出∠ABC与∠EDF的关系,不必说明理由.

分析 (1)图①中由BC∥DE得∠BOD=40°,由DF∥AB得∠EDF=140°;图②中由BC∥DE得∠ABC=∠BOD,再由DF∥AB得∠EDF=∠BOD;
(2)如图③④,根据平行线性质可得;
(3)如图⑤⑥,根据两直线平行,同旁内角互补可得∠EDF=90°.
解答 解:(1)如图①②;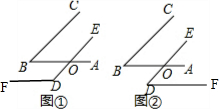
图①中,∵BC∥DE,
∴∠ABC=∠BOD=40°,
∵DF∥AB,
∴∠EDF+∠BOD=180°,
∴∠EDF=180°-40°=140°,
图②中,∵BC∥DE,
∴∠ABC=∠BOD=40°,
∵DF∥AB,
∴∠EDF=∠BOD=40°;
即∠EDF的度数为40°或140°.
(2)如图③④,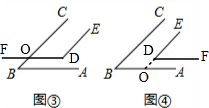
图③中,∠EDF=140°,得:∠ABC+∠EDF=180°,
图④中,∠EDF=40°,得:∠ABC=∠EDF;
(3)如图⑤,图⑥,∠ABC=40°,∠EDF=90°.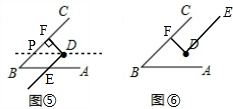
故答案为:(2)∠ABC+∠EDF=180°或∠ABC=∠EDF.
点评 本题主要考查平行线的性质,熟练掌握平行线的性质是根本,结合题意全面画出符合条件的所有图形是关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,在四边形ABCD中,AB=3cm,CD=2cm,∠BAD=60°,∠CDA=∠CBA=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=3cm,CD=2cm,∠BAD=60°,∠CDA=∠CBA=90°,求四边形ABCD的面积.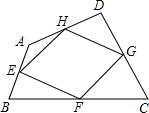 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,请添加一个与四边形ABCD对角线有关的条件,为AC⊥BD,使四边形EFGH是矩形.
如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,请添加一个与四边形ABCD对角线有关的条件,为AC⊥BD,使四边形EFGH是矩形. 如图,在△ABC中,AD⊥BC于D,若∠C=45°,AC=$\sqrt{6}$,BD=1,求AB的长.
如图,在△ABC中,AD⊥BC于D,若∠C=45°,AC=$\sqrt{6}$,BD=1,求AB的长.