题目内容
17.观察下列等式:第1个等式:a1=$\frac{1}{1×3}$=$\frac{1}{2}$(1-$\frac{1}{3}$);第2个等式:a2=$\frac{1}{3×5}$=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$);
第3个等式:a3=$\frac{1}{5×7}$=$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$); 第4个等式:a4=$\frac{1}{7×9}$=$\frac{1}{2}$($\frac{1}{7}$-$\frac{1}{9}$);
…
请解答下列问题:
(1)按以上规律写出第5个等式:a5=$\frac{1}{9×11}$=$\frac{1}{2}$($\frac{1}{9}$-$\frac{1}{11}$).
(2)用含n的式子表示第n个等式:an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$×($\frac{1}{2n-1}$=$\frac{1}{2n+1}$)(n为正整数).
(3)求a1+a2+a3+a4+…+a2016的值.
分析 (1)根据题意得出分母的变化规律,进而得出答案;
(2)根据题意得出分母的变化规律,进而得出答案;
(3)利用(2)中变化规律进而化简求出答案.
解答 解:(1)第5个等式:a5=$\frac{1}{9×11}$=$\frac{1}{2}$($\frac{1}{9}$-$\frac{1}{11}$);
故答案为:$\frac{1}{9×11}$,$\frac{1}{2}$($\frac{1}{9}$-$\frac{1}{11}$);
(2)第n个等式:an=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$×($\frac{1}{2n-1}$=$\frac{1}{2n+1}$);
故答案为:$\frac{1}{(2n-1)(2n+1)}$,$\frac{1}{2}$×($\frac{1}{2n-1}$=$\frac{1}{2n+1}$);
(3)a1+a2+a3+a4+…+a2016
=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+…+$\frac{1}{2}$($\frac{1}{4031}$-$\frac{1}{4033}$)
=$\frac{1}{2}$(1-$\frac{1}{4033}$)
=$\frac{2016}{4033}$.
点评 此题主要考查了分式的加减运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
5.若mn>0,则m,n( )
| A. | m,n一定是正数 | B. | m,n一定是负数 | C. | m,n一定是同号 | D. | m,n一定是异号 |
9.为了了解某班学生每天使用零花钱数(单位:元)的情况,小王随机调查了15名同学,结果如表:
则这15名同学每天使用零花钱的平均数是3元.
| 每天使用零花钱数 | 1 | 2 | 3 | 5 | 6 |
| 人数 | 2 | 5 | 4 | 3 | 1 |
7.不等式3x+10≤1的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
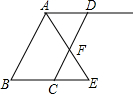 如图,已知AB∥CD,AE平分∠BAD,CD与AE相交于点F.
如图,已知AB∥CD,AE平分∠BAD,CD与AE相交于点F.
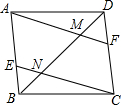 如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.
如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.