题目内容
4.计算题(1)$-\sqrt{3}•\sqrt{(-16)(-36)}$;
(2)$a\sqrt{\frac{3}{a}}+\sqrt{9a}-\frac{{3\sqrt{a}}}{{\sqrt{3}}}$;
(3)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$;
(4)($\sqrt{3}$+1)($\sqrt{3}$-1)+($\sqrt{2}$-1)0-(-$\frac{1}{3}$)-2.
分析 (1)先化简根号内的数,再根据二次根式的乘法进行计算即可解答本题;
(2)先对原式化简,再合并同类项即可解答本题;
(3)先化简括号内的式子,再根据二次根式的除法进行计算即可;
(4)根据平方差公式、零指数幂、负整数指数幂进行计算即可.
解答 解:(1)$-\sqrt{3}•\sqrt{(-16)(-36)}$
=$-\sqrt{3}×\sqrt{16×36}$
=-$\sqrt{3}×24$
=-$24\sqrt{3}$;
(2)$a\sqrt{\frac{3}{a}}+\sqrt{9a}-\frac{{3\sqrt{a}}}{{\sqrt{3}}}$
=$\sqrt{3a}+3\sqrt{a}-\sqrt{3a}$
=$3\sqrt{a}$;
(3)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$
=$(6\sqrt{3}-\frac{2\sqrt{3}}{3}+4\sqrt{3})÷2\sqrt{3}$
=$\frac{28\sqrt{3}}{3}×\frac{1}{2\sqrt{3}}$
=$\frac{14}{3}$;
(4)($\sqrt{3}$+1)($\sqrt{3}$-1)+($\sqrt{2}$-1)0-(-$\frac{1}{3}$)-2
=3-1+1-9
=-6.
点评 本题考查二次根式的混合运算、零指数幂、负整数指数幂,解题的关键是明确它们各自的计算方法,明确二次根式混合运算的计算方法.

练习册系列答案
相关题目
9.某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件,第二个月如果单价不变,预计仍可以售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降1元,可多售出10件,但最低单价应高于购进的价格;第二月结束后.批发商核对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表(不需化简)
(2)如果批发商希望通过销售这批T恤获利8000元,那么第二个月的单价应该是多少?
(3)如果批发商希望通过销售这批T恤获利最大,那么第二个月的单价应是多少元?最大利润为多少?
(1)填表(不需化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量 | 200 | 200+10x | 800-200-(200+10x) |
(3)如果批发商希望通过销售这批T恤获利最大,那么第二个月的单价应是多少元?最大利润为多少?
9.为了了解某班学生每天使用零花钱数(单位:元)的情况,小王随机调查了15名同学,结果如表:
则这15名同学每天使用零花钱的平均数是3元.
| 每天使用零花钱数 | 1 | 2 | 3 | 5 | 6 |
| 人数 | 2 | 5 | 4 | 3 | 1 |
 作图并回答问题.
作图并回答问题.
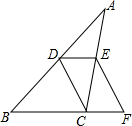 如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=$\frac{1}{2}$BC,连结CD、DE、EF.
如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=$\frac{1}{2}$BC,连结CD、DE、EF.