题目内容
7. 如图,在△ABC中,AD⊥BC于D,若∠C=45°,AC=$\sqrt{6}$,BD=1,求AB的长.
如图,在△ABC中,AD⊥BC于D,若∠C=45°,AC=$\sqrt{6}$,BD=1,求AB的长.
分析 由已知条件得出△ACD是等腰直角三角形,得出AD=$\frac{\sqrt{2}}{2}$AC=$\sqrt{3}$,再在Rt△ABD中,由勾股定理求出AB即可.
解答 解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠C=45°,
∴△ACD是等腰直角三角形,
∴AD=CD=$\frac{\sqrt{2}}{2}$AC=$\sqrt{6}$×$\frac{\sqrt{2}}{2}$=$\sqrt{3}$,
在Rt△ABD中,AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2.
点评 本题考查了勾股定理、等腰直角三角形的判定与性质;熟练掌握勾股定理,证明△ACD是等腰直角三角形得出AD的长是解决问题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
16.数学迷小虎在解方程$\frac{2x-1}{3}=\frac{x+a}{3}$-1去分母时,方程右边的-1漏乘了3,因而求得方程的解为x=-2,请你帮小虎同学求出a的值,并且正确求出原方程的解.
17.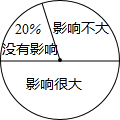 近年来,“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
近年来,“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
(1)求n的值;
(2)统计表中的m=100;
(3)估计该校1800名学生中认为“影响很大”的学生人数.
 近年来,“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
近年来,“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:n名学生对使用计算器影响计算能力的发展看法人数统计表
| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数(人) | 40 | 60 | m |
(2)统计表中的m=100;
(3)估计该校1800名学生中认为“影响很大”的学生人数.
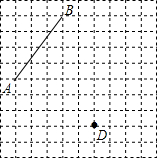 作图并回答问题.
作图并回答问题.