题目内容
3.为了迎接首届中国(太原)煤炭与能源新技术产业博览会的召开,某杜区准备在一块面积为120m2的等腰三角形草坪(其中一边长为20m)的周围围上银白色的低矮栅栏,已知围建这种银白色低矮栅栏每米的费用是a元,求该杜区完成这项工程的总费用.分析 分别利用BC=20m,AB=AC=20m,结合三角形面积以及勾股定理得出三角形的周长即可得出答案.
解答  解:如图1所示:作AD⊥BC于点D,BC=20m,
解:如图1所示:作AD⊥BC于点D,BC=20m,
则$\frac{1}{2}$AD×BC=120,
解得:AD=12,
∵AD⊥BC,AB=AC,
∴BD=DC=10m,
∴AB=AC=$\sqrt{1{0}^{2}+1{2}^{2}}$=2$\sqrt{61}$(m),
故AB+AC+BC=4$\sqrt{61}$+20,
∴该杜区完成这项工程的总费用为:(4$\sqrt{61}$+20)a元;
如图2所示:作AD⊥BC于点D,CE⊥AB于点E,
AB=AC=20m,
则$\frac{1}{2}$AB×EC=120,
解得:CE=12,
∴AE=$\sqrt{2{0}^{2}-{12}^{2}}$=16(m),
∴BE=4m,
∴BC=$\sqrt{{4}^{2}+1{2}^{2}}$=4$\sqrt{10}$(m).
故AB+AC+BC=4$\sqrt{10}$+40,
∴该杜区完成这项工程的总费用为:(4$\sqrt{10}$+40)a元.
点评 此题主要考查了勾股定理的应用,利用分类讨论得出答案是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.2013年4月20日,四川省雅安市芦山县发生了7.0级大地震,给当地居民造成了巨大的损失,“一方有难,八方支援”,某市中学全体师生积极捐款,其中九年级3个班学生的捐款金额如下表:
吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面两条信息:
信息一:这三个班的捐款总金额是7700元;
信息二:九(2)班的捐款金额比九(3)班的捐款金额多300元.
请根据以上信息求出九(2)班与九(3)班的捐款金额各是多少元.
| 班级 | 九(1)班 | 九(2)班 | 九(3)班 |
| 金额/元 | 2000 |
信息一:这三个班的捐款总金额是7700元;
信息二:九(2)班的捐款金额比九(3)班的捐款金额多300元.
请根据以上信息求出九(2)班与九(3)班的捐款金额各是多少元.
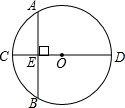 已知:⊙O的半径为6cm,弦AB与直径CD垂直,且将CD分成1:3两部分,求:弦AB的长.
已知:⊙O的半径为6cm,弦AB与直径CD垂直,且将CD分成1:3两部分,求:弦AB的长.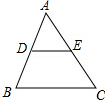 如图,在△ABC中,已知DE∥BC,AD=5,DB=3,BC=10,求:
如图,在△ABC中,已知DE∥BC,AD=5,DB=3,BC=10,求: