题目内容
17.已知a+b=1,ab=1,设s1=a+b,s2=a2+b2,s3=a3+b3,…,sn=an+bn.(1)计算s1=1;s2=3;s3=4;s4=7;
(2)试写出sn-2,sn-1,sn三者之间的关系式Sn-2+Sn-1=Sn;
(3)根据以上得出的结论,计算a10+b10.
分析 (1)利用完全平方公式进行化简,然后代入a+b,ab的值,即可推出结论;
(2)根据(1)所推出的结论,即可推出Sn-2+Sn-1=Sn;
(3)根据(2)的结论,即可推出a10+b10=S10=13S4+8S3.
解答 解:(1)∵s1=a+b=1,S2=a2+b2=(a+b)2-2ab=3;
∵(a2+b2)(a+b)=a3+ab2+a2b+b3=a3+b3+ab(a+b),
∴3×1=a3+b3-1,
∴a3+b3=4,即S3=4,
∵S4=(a2+b2)2-2(ab)2=7,
∴S4=7,
故答案为:1,3,4,7;
(2)∵S2=3,S3=4,S4=7,
∴S2+S3=S4,
∴Sn-2+Sn-1=Sn,
故答案为:Sn-2+Sn-1=Sn;
(3)∵Sn-2+Sn-1=Sn,S2=3,S3=4,S4=7,
∴a10+b10=S10=13S4+8S3=123.
点评 本题主要考查整式的混合运算、完全平方公式的运用,关键在于根据题意推出S2=3,S3=4,S4=7,分析归纳出规律:Sn-2+Sn-1=Sn.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
2. 如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
 如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )| A. | 2.5m | B. | 3m | C. | 3.5m | D. | 4m |
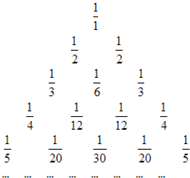 如图所示的数阵叫“莱布尼兹调和三角形”,它们是由正整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如:$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$…,那么第7行第3个数字是$\frac{1}{105}$.
如图所示的数阵叫“莱布尼兹调和三角形”,它们是由正整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如:$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$…,那么第7行第3个数字是$\frac{1}{105}$.
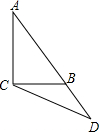 如图,在△ABC中,∠ACB=90°,延长斜边AB到点D,使BD=$\frac{AB}{2}$,连结DC.若tan∠ABC=2,则tan∠BCD的值是$\frac{2}{3}$.
如图,在△ABC中,∠ACB=90°,延长斜边AB到点D,使BD=$\frac{AB}{2}$,连结DC.若tan∠ABC=2,则tan∠BCD的值是$\frac{2}{3}$. 如图,已知抛物线y=x2-2(m+1)x+m2+1与x轴的相交于A,B两点,与y轴交于C(0,5)点,O为原点.
如图,已知抛物线y=x2-2(m+1)x+m2+1与x轴的相交于A,B两点,与y轴交于C(0,5)点,O为原点. 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数y=$\frac{k_2}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OA=OB=2,OD=1.
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数y=$\frac{k_2}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OA=OB=2,OD=1.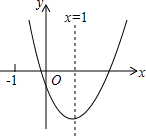 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )