题目内容
7.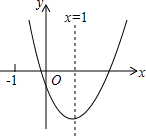 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
分析 根据二次函数的图象的开口向上可得a>0,根据图象y轴的交点在y轴的交点可得c<0,根据对称轴是直线x=1可得b<0,进而可得①正确,再根据函数图象可得x>2时,y有小于0的情况,故②错误,再计算出当x=1时,a-b+c>0,再结合对称轴可得2a+b=0,进而可得3a+c>0;再由2a+b=0,a>0可得3a+b>0.
解答 解:∵二次函数的图象的开口向上,
∴a>0,
∵二次函数的图象y轴的交点在y轴的负半轴上,
∴c<0,
∵二次函数图象的对称轴是直线x=1,
∴-$\frac{b}{2a}$=1,
∴2a+b=0,b<0,
∴abc>0,∴①正确;
∵二次函数y=ax2+bx+c图象可知,当x>2时,y有小于0的情况,
∴②错误;
∵当x=-1时,y>0,
∴a-b+c>0,
把b=-2a代入得:3a+c>0,
∴③正确;
∵二次函数图象的对称轴是直线x=1,
∴-$\frac{b}{2a}$=1,
∴2a+b=0,
∵a>0,
∴3a+b>0,故④正确.
故选C.
点评 此题考查了二次函数图象与系数的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,关键是数熟练掌握二次函数的性质.

练习册系列答案
相关题目
18.二次函数y=ax2+bx+c(a≠0)对于x的任何值都恒为负值的条件是( )
| A. | a>0,?△>0 | B. | a>0,?△<0 | C. | a<0,?△>0 | D. | a<0,?△<0 |
2.在下列各数-$\frac{22}{7}$,0,1.5,-3,5$\frac{1}{2}$,50%,+8中,是整数的有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
19.下列各数在数轴上的位置是在-2的左边的是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
16.若分式$\frac{2x+1}{{x}^{2}}$的值为正,则x的取值范围是( )
| A. | x>0 | B. | x>-$\frac{1}{2}$ | C. | x≠-$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$且x≠0 |
18.小芳有两根长度为4cm和9cm的木条,他想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择的木条的长度只能是( )
| A. | 5 cm | B. | 3 cm | C. | 17 cm | D. | 12 cm |
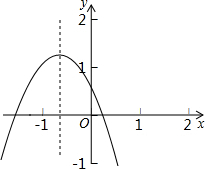 如图所示的二次函数y═ax2+bx+c的图象,下列结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0,其中正确的有( )
如图所示的二次函数y═ax2+bx+c的图象,下列结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0,其中正确的有( )