题目内容
7.(1)阅读下面材料: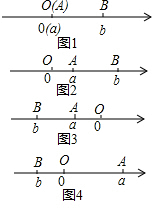
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4;
②数轴上表示x和-1的两点A和B之间的距离是|x+1|,如果|AB|=2,那么x为1或-3;
③代数式|x+1|+|x-2|取最小值时,相应的整数x的取值是-1、0、1、2.
分析 根据题意给出的数量关系即可求出答案.
解答 解:(2)|x+1|=2,
∴x+1=±2,
∴x=1或-3,
(3)由题意可知:|x+1|+|x-2|表示数x到-1和2之间的距离之和,
∴当-1≤x≤2时,
∴|x+1|+|x-2|可取得最小值,
∴x的整数位-1,0,1,2;
故答案为:
(1)3;3;4
(2)|x+1|;1或-3
(3)-1,0,1,2
点评 本题考查绝对值的定义,由于文字信息较大,考查学生阅读理解能力.

练习册系列答案
相关题目
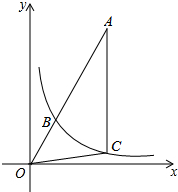 反比例函数y=$\frac{k}{x}$ (x>0)的图象如图,点B在图象上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交y=$\frac{k}{x}$(x>0)的图象于点C,连接OC,S△AOC=5,求k值.
反比例函数y=$\frac{k}{x}$ (x>0)的图象如图,点B在图象上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交y=$\frac{k}{x}$(x>0)的图象于点C,连接OC,S△AOC=5,求k值.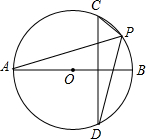 如图AB是⊙O的直径,CD是⊙O的弦,CD垂直AB,P是弧CD上的一点(不与C、D重合),∠APC与∠APD相等吗?为什么?
如图AB是⊙O的直径,CD是⊙O的弦,CD垂直AB,P是弧CD上的一点(不与C、D重合),∠APC与∠APD相等吗?为什么? 如图所示,BE=CF,DE⊥AB于E,DF⊥AC于F,且BD=CD,AD是∠BAC的平分线吗?为什么?
如图所示,BE=CF,DE⊥AB于E,DF⊥AC于F,且BD=CD,AD是∠BAC的平分线吗?为什么?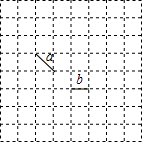 如图是8×8的格点,线段a、b的端点在格点上,请在图中画出第三条线段,使其端点在格点上且与线段a、b组成轴对称图形.(画出所有情况,并在图中把这些线段标记为线段c、d、e、f、g….)
如图是8×8的格点,线段a、b的端点在格点上,请在图中画出第三条线段,使其端点在格点上且与线段a、b组成轴对称图形.(画出所有情况,并在图中把这些线段标记为线段c、d、e、f、g….)