题目内容
5.已知点A(x1,y1)、B(x2,y2)、C(x3,y3)是函数y=-$\frac{2}{x}$图象上的点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y1>y3>y2 | D. | 无法确定 |
分析 根据反比例函数图象上点的坐标特征得到y1=-$\frac{2}{{x}_{1}}$,y2=-$\frac{2}{{x}_{2}}$,y3=-$\frac{2}{{x}_{3}}$,然后根据x1<0<x2<x3比较y1,y2,y3的大小.
解答 解:点(x1,y1),(x2,y2),(x3,y3)都是y=-$\frac{2}{x}$的图象上的点,
∴y1=-$\frac{2}{{x}_{1}}$,y2=-$\frac{2}{{x}_{2}}$,y3=-$\frac{2}{{x}_{3}}$,
而x1<0<x2<x3,
∴y3<y2<y1.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
13.下列各数:-(-2),-|-2|,(-2)2,-22,(-2)3,-23,负数个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
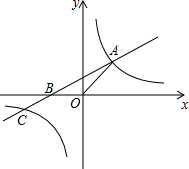 如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=$\frac{4}{x}$交于点A、C,其中点A在第一象限,点C在第三象限.
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=$\frac{4}{x}$交于点A、C,其中点A在第一象限,点C在第三象限.

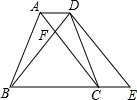 如图所示,梯形ABCD中,已知:AD∥BC,∠ABC=∠DCB,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD.
如图所示,梯形ABCD中,已知:AD∥BC,∠ABC=∠DCB,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD.