题目内容
15.因式分解:a3b-ab3+a2+b2+1.分析 首先分组进而补项,进而分解因式得出即可.
解答 解:a3b-ab3+a2+b2+1
=a3b-a2b2+a2b2+ab-ab-ab3+a2+b2+1
=a3b-a2b2+ab+a2b2-ab3+b2+a2-ab+1
=ab(a2-ab+1)+b2(a2-ab+1)+(a2-ab+1)
=(a2-ab+1)(ab+b2+1).
点评 此题主要考查了分组分解法分解因式,正确利用补项法分解因式是解题关键.

练习册系列答案
相关题目
10.如果xy≠0,$\frac{1}{3}$xy2+axy2=0,那么a的值为( )
| A. | 0 | B. | 3 | C. | -3 | D. | -$\frac{1}{3}$ |
5.已知点A(x1,y1)、B(x2,y2)、C(x3,y3)是函数y=-$\frac{2}{x}$图象上的点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y1>y3>y2 | D. | 无法确定 |
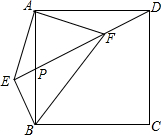 如图,在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE,FA⊥AE交DP于点F,连接BF、FC.若AE=4,则FC=4$\sqrt{2}$.
如图,在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE,FA⊥AE交DP于点F,连接BF、FC.若AE=4,则FC=4$\sqrt{2}$.