题目内容
19. 如图,已知点D是△ABC的边AC上的一点,连接BD.∠ABD=∠C,AB=6,AD=4.
如图,已知点D是△ABC的边AC上的一点,连接BD.∠ABD=∠C,AB=6,AD=4.(1)求证:△ABD∽△ACB;
(2)求线段CD的长.
分析 (1)根据∠ABD=∠C,∠A=∠A,即可证得△ABD∽△ACB;
(2)由(1)知:△ABD∽△ACB,根据相似三角形的性质得到$\frac{AD}{AB}$=$\frac{AB}{AC}$,代入数据即可得到结果.
解答 解:(1)∵∠ABD=∠C,∠A=∠A(公共角),
∴△ABD∽△ACB;
(2)由(1)知:△ABD∽△ACB,
∴$\frac{AD}{AB}$=$\frac{AB}{AC}$,
即$\frac{4}{6}$=$\frac{6}{4+CD}$,
∴CD=5.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
14. 如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
 如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )| A. | ①②④ | B. | ①③ | C. | ①④ | D. | ①③④ |
11.如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前m个格子中所填整数之和是2014,则m的值为( )
| 9 | a | b | c | -5 | 1 | … |
| A. | 2015 | B. | 1008 | C. | 1208 | D. | 2008 |
8.下列各对数中,数值相等的是( )
| A. | (2)3和(-3)2 | B. | -32和(-3)2 | C. | -33和(-3)3 | D. | -3×23和(-3×2)3 |
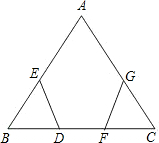 如图,一个特大型设备人字梁,工人师傅要检查人字梁的AB和AC是否相等,但是他直接测量不方便,身边只有一个刻度尺(长度远远不够).它是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长a米,FG的长b米,如果a=b,则说明AB和AC是相等的,他的这种做法合理吗?为什么?
如图,一个特大型设备人字梁,工人师傅要检查人字梁的AB和AC是否相等,但是他直接测量不方便,身边只有一个刻度尺(长度远远不够).它是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长a米,FG的长b米,如果a=b,则说明AB和AC是相等的,他的这种做法合理吗?为什么?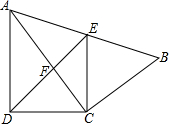 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点.