题目内容
4．已知一直角三角形的木板，三边的平方和为1800cm2，则斜边长为（ ）| A． | 30cm | B． | 80cm | C． | 90cm | D． | 120cm |
分析 先求出斜边的平方，进而可得出结论．
解答 解：设直角三角形的斜边长为x，
∵三边的平方和为1800cm2，
∴x2=900cm2，解得x=30cm．
故选A．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．用配方法解方程x2-8x+3=0，下列变形正确的是（ ）
| A． | （x+4）2=13 | B． | （x-4）2=19 | C． | （x-4）2=13 | D． | （x+4）2=19 |
12．方程（x+1）（x-2）=0的两根分别为（ ）
| A． | x1=1，x2=2 | B． | x1=-1，x2=-2 | C． | x1=1，x2=-2 | D． | x1=-1，x2=2 |
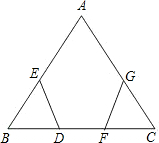如图，一个特大型设备人字梁，工人师傅要检查人字梁的AB和AC是否相等，但是他直接测量不方便，身边只有一个刻度尺（长度远远不够）．它是这样操作的：①分别在BA和CA上取BE=CG；②在BC上取BD=CF；③量出DE的长a米，FG的长b米，如果a=b，则说明AB和AC是相等的，他的这种做法合理吗？为什么？
13．下列各组单项式中，属同类项的是（ ）
| A． | a与$\frac{a}{2}$ | B． | 5ab与5abc | C． | $\frac{1}{2}$m2n与$\frac{1}{2}$mn | D． | x3与23 |
如图，AB是⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，且∠BAC=50°，给出下列四个结论：①BD=CD，②AE=CE，③∠ABE=40°，④劣弧DE的度数为25°．其中正确结论的序号是（ ）