题目内容
18.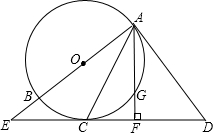 如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.
如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.求证:DE是⊙O的切线.
分析 由切线的性质得出∠OAD=90°,即∠1+∠DAC=90°,再由OA=OC得出∠1=∠2,得出∠2+∠ACD=∠1+∠DAC=90°,即DE⊥OC,即可证出结论.
解答 证明:连接OC,如图所示: ∵直线AD与⊙O相切于点A,
∵直线AD与⊙O相切于点A,
∴AD⊥OA,
∴∠OAD=90°,即∠1+∠DAC=90°,
∵OA=OC,
∴∠1=∠2,
又∵∠DAC=∠ACD,
∴∠2+∠ACD=∠1+∠DAC=90°,
即DE⊥OC,
∴DE是⊙O的切线.
点评 本题考查了切线的性质与判定;熟练掌握切线的性质与判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
18. 如图,直线l1、l2交于点O,则到l1、l2的距离分别为2和1的点有( )个.
如图,直线l1、l2交于点O,则到l1、l2的距离分别为2和1的点有( )个.
 如图,直线l1、l2交于点O,则到l1、l2的距离分别为2和1的点有( )个.
如图,直线l1、l2交于点O,则到l1、l2的距离分别为2和1的点有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.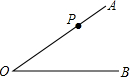 如图,P为∠AOB边OA上一点,∠AOB=30°,OP=10cm,以P为圆心,5cm为半径的圆与直线OB的位置关系是( )
如图,P为∠AOB边OA上一点,∠AOB=30°,OP=10cm,以P为圆心,5cm为半径的圆与直线OB的位置关系是( )
 如图,P为∠AOB边OA上一点,∠AOB=30°,OP=10cm,以P为圆心,5cm为半径的圆与直线OB的位置关系是( )
如图,P为∠AOB边OA上一点,∠AOB=30°,OP=10cm,以P为圆心,5cm为半径的圆与直线OB的位置关系是( )| A. | 相离 | B. | 相交 | C. | 相切 | D. | 无法确定 |
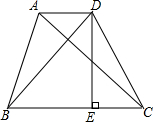 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,DE是梯形的高,若S梯形ABCD=49cm2,求梯形的高.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,DE是梯形的高,若S梯形ABCD=49cm2,求梯形的高.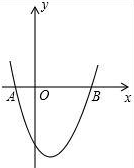 如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.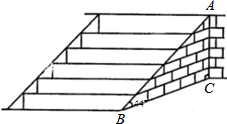 武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).
武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).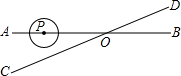 如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )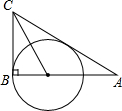 如图,在Rt△ABC中,∠ABC=90°,∠ACB的平分线CO交AB边于点O,以点O为圆心,OB为半径作⊙O.
如图,在Rt△ABC中,∠ABC=90°,∠ACB的平分线CO交AB边于点O,以点O为圆心,OB为半径作⊙O.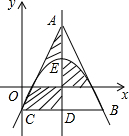 如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$.
如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$.