题目内容
8.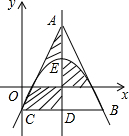 如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$.
如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$.
分析 根据抛物线的对称性可知图中阴影部分图形的面积之和=S△ACD=$\frac{1}{2}$S△ABC.
解答 解:∵AD是抛物线y=a(x-2)2+k的对称轴,△ABC是等边三角形,
∴图中阴影部分图形的面积之和=S△ACD=$\frac{1}{2}$S△ABC.
∵CD=2,
∴BC=2CD=4,
∴S△ABC=$\frac{\sqrt{3}}{4}$×42=4$\sqrt{3}$,
∴图中阴影部分图形的面积之和=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查了二次函数的性质,等边三角形的面积,根据抛物线的对称性得出图中阴影部分图形的面积之和=S△ACD是解题的关键.

练习册系列答案
相关题目
19.若x轴上的点P到y轴的距离为2015,则点P的坐标是( )
| A. | (2015,0) | B. | (0,2015) | C. | (2015,0)或(-2015,0) | D. | (0,2015)或(0,-2015) |
3.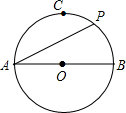 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )
 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )| A. | 0° | B. | 30° | C. | 45° | D. | 60° |
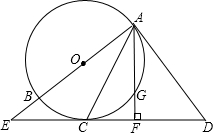 如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.
如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.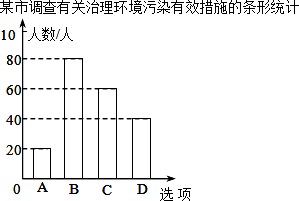 某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):
某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):
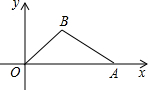 如图,在平面直角坐标系内,O为原点,点A在x轴正半轴上,点B(4,3),
如图,在平面直角坐标系内,O为原点,点A在x轴正半轴上,点B(4,3),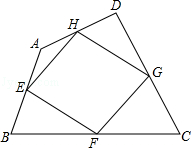 如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.