题目内容
7.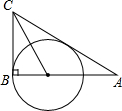 如图,在Rt△ABC中,∠ABC=90°,∠ACB的平分线CO交AB边于点O,以点O为圆心,OB为半径作⊙O.
如图,在Rt△ABC中,∠ABC=90°,∠ACB的平分线CO交AB边于点O,以点O为圆心,OB为半径作⊙O.(1)请判断AC与⊙O的位置关系,并证明你的结论;
(2)若BO=1,∠BAC=30°,求△AOC的面积.
分析 (1)过点O作OE⊥AC于点E,由CO平分∠ACB,得出OE=OB,即可证出结论;
(2)先根据勾股定理求出BC,再求出AC,即可得出结果.
解答 (1)解:AC与⊙O相切,理由如下:
过点O作OE⊥AC于点E,如图所示: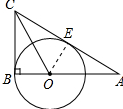
∵∠ABC=90°,CO平分∠ACB,
∴OE=OB,
∴AC是⊙O的切线;
(2)解:∵∠A=30°,∠ABC=90°,
∴∠ACB=60°,
∵CO平分∠ACB,
∴∠OCB=30°,
∵在Rt△BCO中,BO=1,
∴OC=2,$BC=\sqrt{4-1}=\sqrt{3}$,
∵∠A=30°,
∴AC=2BC=$2\sqrt{3}$,
∴${S_{△AOC}}=\frac{1}{2}AC•OE=\frac{1}{2}AC•OB=\frac{1}{2}×2\sqrt{3}×1=\sqrt{3}$.
点评 本题考查了切线的判定、角平分线的性质、勾股定理的运用以及三角形面积的计算;熟练掌握切线的判定方法,并能进行有关运算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列说法正确的是( )
| A. | 一组数据8,8,7,10,6,8,9的众数和中位数都是8 | |
| B. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| C. | 一个游戏的中奖概率是0.1,则做10次这样的游戏一定会中奖 | |
| D. | 若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定 |
19.若x轴上的点P到y轴的距离为2015,则点P的坐标是( )
| A. | (2015,0) | B. | (0,2015) | C. | (2015,0)或(-2015,0) | D. | (0,2015)或(0,-2015) |
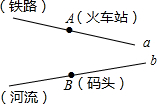 火车站,码头分别位于A,B两点,直线a,b分别表示铁路与河流
火车站,码头分别位于A,B两点,直线a,b分别表示铁路与河流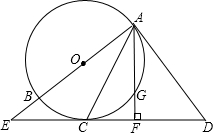 如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.
如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.
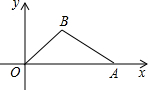 如图,在平面直角坐标系内,O为原点,点A在x轴正半轴上,点B(4,3),
如图,在平面直角坐标系内,O为原点,点A在x轴正半轴上,点B(4,3),