题目内容
19.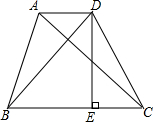 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,DE是梯形的高,若S梯形ABCD=49cm2,求梯形的高.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,DE是梯形的高,若S梯形ABCD=49cm2,求梯形的高.
分析 作辅助线:延长CB至E,使DB∥AE,则根据已知条件,可构建平行四边形ADBE和等腰直角△EAC,则直角△AEC的面积等于梯形ABCD的面积,利用高AF表示出△ACE的面积,即可求解.
解答 解:延长CB至E,使DB∥AE.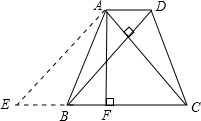
∵AC⊥BD,
∴AE⊥AC.
∵AD∥BC,DB∥AE,
∴四边形ADBE为平行四边形.
∴DB=AE,AD=EB,
∵四边形ABCD是等腰梯形,
∴DB=AC,
∴AE=AC,
∴△AEC为等腰直角三角形.
∵S梯形=$\frac{1}{2}$=49.
∵S△AEC=$\frac{1}{2}$=$\frac{1}{2}$=$\frac{1}{2}$,
∴S梯形=S△AEC
∴$\frac{1}{2}$AE2=49.
∴AE2=98.
∵AF⊥EC,
∴AF=FE.
∴2AF2=AE2
∴AF=7.
点评 此题关键是作辅助线,构建等腰直角三角形AEC,将等腰梯形的面积转化到等腰直角三角形中,根据等腰梯形、平行四边形性质及等腰直角三角形的性质求解.

练习册系列答案
相关题目
9.|-$\frac{2}{3}$|=( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
19.若x轴上的点P到y轴的距离为2015,则点P的坐标是( )
| A. | (2015,0) | B. | (0,2015) | C. | (2015,0)或(-2015,0) | D. | (0,2015)或(0,-2015) |
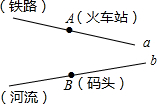 火车站,码头分别位于A,B两点,直线a,b分别表示铁路与河流
火车站,码头分别位于A,B两点,直线a,b分别表示铁路与河流
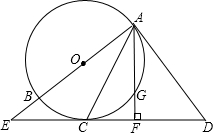 如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.
如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.