题目内容
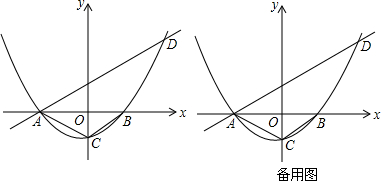
19.如图,抛物线y=ax2+bx+c(a>0)的图象与x轴交于A(一4,0)、B(2,0),与y轴交于点C.经过点A的直线y=$\frac{1}{2}$x+2与抛物线的另一个交点为D,点P是抛物线上的一个动点.(1)b=2a,C=-8a(用含a的代数式表示);
(2)若点D的横坐标为5,求抛物线的解析式;
(3)在(2)的条件下,在直线AD下方的抛物线上求点P,使△APD的面积等于$\frac{21}{2}$;
(4)若在第二象限内的抛物线上存在动点P,使得以A、B、P为顶点的三角形与△ABC相似,求a的值.
分析 (1)把A与B的坐标代入抛物线解析式得到方程组,将a看做已知数表示出b与c即可;
(2)把x=5代入直线解析式求出y的值,确定出D坐标,设出抛物线解析式,把D坐标代入求出a的值,确定出抛物线解析式即可;
(3)过点P作PE⊥x轴,交AD于点E,设出P坐标,进而表示出E坐标,根据P在直线AD下方,表示出PE的长,由三角形APD面积列出关于x的方程,求出方程的解得到x的值,即可确定出P的坐标;
(4)设P坐标为(x,y),分两种情况考虑:①若△PAB∽△BAC,可得∠PBA=∠BAC,进而确定出tan∠PBA=tan∠BAC,利用锐角三角函数定义表示出y与x的关系式,与抛物线解析式联立表示出x与y,利用勾股定理表示出PB与AC,由相似得比例列出关于a的方程,求出方程的解即可得到a的值;②若△PAB∽△ACB,则∠PBA=∠ABC,同理求出a的值即可.
解答 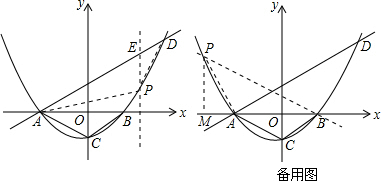 解:(1)把A(-4,0)和B(2,0)代入抛物线解析式得:$\left\{\begin{array}{l}{16a-4b+c=0}\\{4a+2b+c=0}\end{array}\right.$,
解:(1)把A(-4,0)和B(2,0)代入抛物线解析式得:$\left\{\begin{array}{l}{16a-4b+c=0}\\{4a+2b+c=0}\end{array}\right.$,
解得:b=2a,c=-8a;
故答案为:2a;-8a;
(2)把x=5代入y=$\frac{1}{2}$x+2得:y=$\frac{9}{2}$,即D(5,$\frac{9}{2}$),
根据题意设抛物线解析式为y=a(x+4)(x-2),
把D(5,$\frac{9}{2}$)代入得:$\frac{9}{2}$=a(5+4)(5-2),
解得:a=$\frac{1}{6}$,
则抛物线解析式为y=$\frac{1}{6}$(x+4)(x-2)=$\frac{1}{6}$x2+$\frac{1}{3}$x-$\frac{4}{3}$;
(3)过点P作PE⊥x轴,交AD于点E,
设点P坐标为(x,$\frac{1}{6}$x2+$\frac{1}{3}$x-$\frac{4}{3}$),则点E坐标为(x,$\frac{1}{2}$x+2),
∵点P在直线AD的下方,
∴PE=$\frac{1}{2}$x+2-($\frac{1}{6}$x2+$\frac{1}{3}$x-$\frac{4}{3}$)=-$\frac{1}{6}$x2+$\frac{1}{6}$x+$\frac{10}{3}$,
∵△APD面积为$\frac{21}{2}$,
∴$\frac{1}{2}$×PE×9=$\frac{21}{2}$,即$\frac{1}{2}$(-$\frac{1}{6}$x2+$\frac{1}{6}$x+$\frac{10}{3}$)×9=$\frac{21}{2}$,
整理得:x2-x-6=0,即(x-3)(x+2)=0,
解得:x=3或x=-2,
则点P的坐标为(3,$\frac{7}{6}$)或(-2,-$\frac{4}{3}$);
(4)设点P的坐标为(x,y),
①若△PAB∽△BCA,则∠PBA=∠BCA,
∴tan∠PBA=tan∠BCA,即$\frac{y}{2-x}$=$\frac{8a}{4}$,
整理得:y=-2a(x-2),
联立得:$\left\{\begin{array}{l}{y=-2x(x-2)}\\{y=a(x+4)(x-2)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-6}\\{y=16a}\end{array}\right.$,
由勾股定理得:PB=$\sqrt{64+256{a}^{2}}$,AC=$\sqrt{16+64{a}^{2}}$,
∵△PAB∽△BAC,
∴$\frac{AC}{AB}$=$\frac{BA}{BP}$,即$\frac{\sqrt{16+64{a}^{2}}}{6}$=$\frac{6}{\sqrt{64+256{a}^{2}}}$,
解得:a=$\frac{\sqrt{2}}{8}$;
②若△PAB∽△ACB,则∠PBA=∠ABC,
∴tan∠PBA=tan∠ABC,
∴$\frac{y}{2-x}$=$\frac{8a}{2}$,即y=-4a(x-2),
联立得:$\left\{\begin{array}{l}{y=-4a(x-2)}\\{y=a(x+4)(x-2)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-8}\\{y=40a}\end{array}\right.$,
由勾股定理得:PB=$\sqrt{100+1600{a}^{2}}$,BC=$\sqrt{4+64{a}^{2}}$,
∵△PAB∽△ACB,
∴$\frac{BC}{BA}$=$\frac{BA}{BP}$,即$\frac{\sqrt{4+64{a}^{2}}}{6}$=$\frac{6}{\sqrt{100+1600{a}^{2}}}$,
解得:a=$\frac{\sqrt{5}}{10}$.
点评 此题属于二次函数综合题,涉及的知识有:待定系数法求函数解析式,二元一次方程组的解法,勾股定理,相似三角形的判定与性质,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案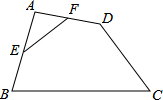 如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则sinC等于( )
如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则sinC等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
| A. | 5.464×10-7 | B. | 5.464×10-8 | C. | 5.464×10-9 | D. | 5.464×10-10 |
| A. |  | B. | 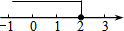 | C. | 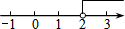 | D. |  |
| A. | (-x-y)(-x+y)=x2-y2 | B. | $\frac{1}{x}$-x=$\frac{1-x}{x}$ | C. | x2-4x+3=(x-2)2+1 | D. | x÷(x2+x)=$\frac{1}{x}$+1 |
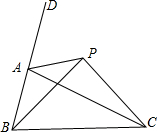 如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.
如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.