题目内容
20.若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=-1,则使函数值y>0成立的x的取值范围是( )| A. | x<-4或x>2 | B. | -4≤x≤2 | C. | x≤-4或x≥2 | D. | -4<x<2 |
分析 由抛物线与x轴的交点及对称轴求出另一个交点坐标,根据抛物线开口向下,根据图象求出使函数值y>0成立的x的取值范围即可.
解答 解:∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=-1,
∴二次函数的图象与x轴另一个交点为(-4,0),
∵a<0,
∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是-4<x<2.
故选D.
点评 此题考查了二次函数与不等式(组),求出抛物线与x轴另一个交点坐标是解本题的关键.

练习册系列答案
相关题目
11.不等式x-2≤0的解集在以下数轴表示中正确的是( )
| A. |  | B. | 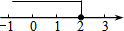 | C. | 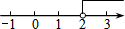 | D. | 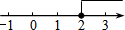 |
12.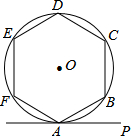 如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
 如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )| A. | 30° | B. | 35° | C. | 45° | D. | 60° |
9.下列各式的变形中,正确的是( )
| A. | (-x-y)(-x+y)=x2-y2 | B. | $\frac{1}{x}$-x=$\frac{1-x}{x}$ | C. | x2-4x+3=(x-2)2+1 | D. | x÷(x2+x)=$\frac{1}{x}$+1 |
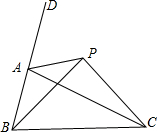 如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.
如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.
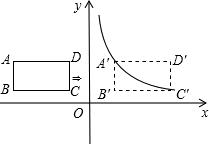 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.
如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.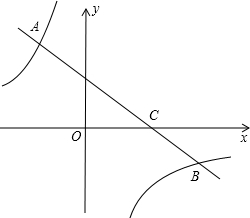 如图,一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
如图,一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.