题目内容
11.某公司生产的A种产品,每件成本是2元,每件售价是3元,一年的销售量是10万件.为了获得更多的利润,公司准备拿出一定资金来做广告.根据经验,每年投入的广告费为x(万元)时,产品的年销售量是原来的y倍,且y是x的二次函数,公司作了预测,知x与y之间的对应关系如表:| x(万元) | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
(2)如果把利润看成是销售总额减去成本和广告费,请你写出年利润S(万元)与广告费x(万元)的函数关系式;
(3)根据上面的函数关系式,你认为每年投入多少广告费最合适?为什么?
分析 (1)设所求函数关系式为y=ax2+bx+c,由表中数据用待定系数法可求得解析式;
(2)根据:总利润=每件利润×销售量-广告费列函数关系式即可;
(3)将(2)中函数关系式配方成顶点式,可知获得最大利润时投入的广告费x.
解答 解:(1)设所求函数关系式为y=ax2+bx+c,
把(0,1),(1,1.5),(2,1.8)分别代入上式,
得:$\left\{\begin{array}{l}{c=1}\\{a+b+c=1.5}\\{4a+2b+c=1.8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{10}}\\{b=\frac{3}{5}}\\{c=1}\end{array}\right.$,
∴y=-$\frac{1}{10}$x2+$\frac{3}{5}$x+1;
(2)根据题意,有:S=(3-2)×10y-x
=(-$\frac{1}{10}$x2+$\frac{3}{5}$x+1)×10-x
=-x2+5x+10;
(3)∵S=-x2+5x+10=-(x-$\frac{5}{2}$)2+$\frac{65}{4}$,
∴每年投入广告费为2.5万元最合适,因为此时可获最大利润.
点评 本题主要考查二次函数的应用,待定系数法求解析式是解题的基础和前提,利润问题中准确确定相等关系是解题的关键.

练习册系列答案
相关题目
16.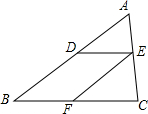 如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
 如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
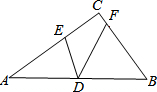 如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2$\sqrt{2}$,DF=4,则AB的长为4$\sqrt{5}$.
如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2$\sqrt{2}$,DF=4,则AB的长为4$\sqrt{5}$.