题目内容
8.已知点(-2,y1),(-3,y2),(1,y3)在函数y=2x2+8x+7的图象上.则y1、y2、y3的大小关系是( )| A. | y3<y2<y1 | B. | y2<y3<y1 | C. | y1<y2<y3 | D. | y1<y3<y2 |
分析 先求出二次函数y=2x2+8x+7的图象的对称轴,然后判断出A(-2,y1),B(-3,y2),C(1,y3)在抛物线上的位置,再求解.
解答 解:∵二次函数y=2x2+8x+7中a=2>0,
∴开口向上,对称轴为x=-2,
∵(-2,y1)中x=-2,y1最小,(1,y3),点B关于对称轴的对称点B′横坐标是2×(-2)-1=-5,则有B′(-5,y3),因为在对称轴得右侧,y随x得增大而增大,故y3>y2.
∴y3>y2>y1.
故选C.
点评 此题考查二次函数图象上点的坐标特征,关键是掌握二次函数图象的性质.

练习册系列答案
相关题目
16.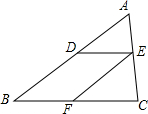 如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
 如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |

 如图,要使AB∥CD,只需要添加一个条件,这个条件是∠ABD=∠BDC(填一个你认为正确的条件即可).
如图,要使AB∥CD,只需要添加一个条件,这个条件是∠ABD=∠BDC(填一个你认为正确的条件即可).