题目内容
 已知:如图,在Rt△ABC中,∠ACB=90°,CA=CB,O是AB的中点,点D在BA的延长线上,以D为直角顶点作RT△DEF,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断段OM、ON的数量关系与位置关系,并写出证明过程.
已知:如图,在Rt△ABC中,∠ACB=90°,CA=CB,O是AB的中点,点D在BA的延长线上,以D为直角顶点作RT△DEF,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断段OM、ON的数量关系与位置关系,并写出证明过程.考点:全等三角形的判定与性质,等腰直角三角形
专题:计算题
分析:OM=ON,OM⊥ON.理由如下:连接CO,则CO为AB边长的中线,利用直角三角形中斜边上的中线等于斜边的一半得到OC=OB,再由CA=CB,得到∠CAB=∠B=45,∠1=∠2=45°,∠AOC=∠BOC=90°,进而得到∠2=∠B,得到四边形DMCN为矩形,得到DN=MC,MC=NB,且夹角相等,利用SAS得到三角形MOC与三角形NOB全等,利用全等三角形的对应边相等得到OM=ON,∠MOC=∠NOB,利用等式的性质得到OM⊥ON.
解答: 解:OM=ON,OM⊥ON.理由如下:
解:OM=ON,OM⊥ON.理由如下:
连接CO,则CO是AB边上的中线,
∵∠ACB=90°,
∴OC=
AB=OB,
又∵CA=CB,
∴∠CAB=∠B=45,∠1=∠2=45°,∠AOC=∠BOC=90°,
∴∠2=∠B,
∵BN⊥DE,
∴∠BND=90°,
又∵∠B=45°,
∴∠3=45°,
∴∠3=∠B,
∴DN=NB,
∵∠ACB=90°,
∴∠NCM=90°,
又∵BN⊥DE,
∴∠DNC=90°
∴四边形DMCN是矩形,
∴DN=MC,
∴MC=NB,
∴△MOC≌△NOB(SAS),
∴OM=ON,∠MOC=∠NOB,
∴∠MOC-∠CON=∠NOB-∠CON,即∠MON=∠BOC=90°,
∴OM⊥ON.
 解:OM=ON,OM⊥ON.理由如下:
解:OM=ON,OM⊥ON.理由如下:连接CO,则CO是AB边上的中线,
∵∠ACB=90°,
∴OC=
| 1 |
| 2 |
又∵CA=CB,
∴∠CAB=∠B=45,∠1=∠2=45°,∠AOC=∠BOC=90°,
∴∠2=∠B,
∵BN⊥DE,
∴∠BND=90°,
又∵∠B=45°,
∴∠3=45°,
∴∠3=∠B,
∴DN=NB,
∵∠ACB=90°,
∴∠NCM=90°,
又∵BN⊥DE,
∴∠DNC=90°
∴四边形DMCN是矩形,
∴DN=MC,
∴MC=NB,
∴△MOC≌△NOB(SAS),
∴OM=ON,∠MOC=∠NOB,
∴∠MOC-∠CON=∠NOB-∠CON,即∠MON=∠BOC=90°,
∴OM⊥ON.
点评:此题考查了全等三角形的判定与性质,以及等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
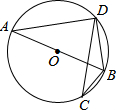 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD等于( )
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD等于( )| A、112° | B、34° |
| C、56° | D、68° |
 如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车
如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车 某市拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图,请利用尺规作图找出音乐喷泉M的位置(要求:不写已知、求作、作法和结论,保留作图痕迹);连结AM、CM,则AM
某市拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图,请利用尺规作图找出音乐喷泉M的位置(要求:不写已知、求作、作法和结论,保留作图痕迹);连结AM、CM,则AM 如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,EF为折痕,D′F与BC交于点G.试判断∠A′EB与∠BGD′之间的数量关系,并加以证明.
如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,EF为折痕,D′F与BC交于点G.试判断∠A′EB与∠BGD′之间的数量关系,并加以证明.